CS-121 / CSCI-E121 Lecture 2
N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 2: Some nice math
Boaz Barak (instructor), Salil Vadhan (co-instructor), Juan Perdomo (Head TF), and many more.
Slides will be posted online.
No polls today, but have pen and paper

Laptops/phones only on last 3 rows please.
Plan for today
- A tour of some discrete math
- Non exhaustive
- Meet again some of those later on
Too fast for some, too slow for others - differences will shrink with time and practice
Consider attending proof workshop, especially if didn’t take Math 23/25 or CS 20
Math is like..
Lego bricks, Russian dolls, Constructing a building, …

Math is like..
Building an iPhone App

Every layer builds on the one below.
Often can ignore implementation: focus on how to use it and not what it is made of. (but not always!)
Best Engineers know every layer, and also know which details to ignore in which context. (and how to pick up new tools as needed)
Example
Graphs are made out of sets and tuples.
Need to know the definition, but more importantly the usage.
The mathematical approach:
- Take concept we want to model (number, triangle, graph, algorithm,..) and give precise definition.
- Use definition to prove properties of this concept.
- Use properties to build higher level objects.
See Mathematics: A very short introduction / Tim Gowers, Ahlfors lecturer 10/11-12
Today’s lecture
- Graphs
- Proofs
- Functions
- Asymptotics
Graphs
Graphs
- Universe of potential objects
- Some of them are related to one anothers.
Examples:
- Social network: \(u \sim v\) is \(u\) and \(v\) are Facebook friends
- Road network: \(u \sim v\) if \(u\) and \(v\) are nearby intersections.
- Course prerequisites: \(\overrightarrow{u v}\) if \(u\) must be taken before \(v\).
- Web graph: \(\overrightarrow{u v}\) if \(u\) links to \(v\).
- Feature correlation graph: \(u \sim v\) if they appear together in the data.
- Disease gene graph: \(u \sim v\) if \(u\) is a gene that is associated with the disease \(v\).
Definition and example
A directed graph consists of vertices \(V\) and edges \(E \subseteq V \times V\) (ordered pairs of vertices)
A cycle is a list \((v_0,v_1,\ldots,v_k) \in V^{k+1}\) s.t. \((v_i,v_{i+1}) \in E\) for all \(i\in [k]\) and \(v_k=v_0\).
Definition and example
A directed graph consists of vertices \(V\) and edges \(E \subseteq V \times V\) (ordered pairs of vertices)
A cycle is a list \((v_0,v_1,\ldots,v_k) \in V^{k+1}\) s.t. \((v_i,v_{i+1}) \in E\) for all \(i\in [k]\) and \(v_k=v_0\).
A DAG is directed graph with no cycles. (i.e., course prerequisite graphs)
Topological Sort Thm: For every \(n\)-vertex directed \(G=(V,E)\), \(G\) is acyclic if and only if can sort \(V\) so edges only increase. That is, exists \(f:V \rightarrow [n]\) s.t. \(f(u) \lt f(v)\) for every \(\overrightarrow{u v}\)
Prove in pairs: The “only if” direction for \(n=3\) (try \(n=4\) or all \(n\))
Proof idea
Topological Sort Thm: For every \(n\)-vertex directed \(G=(V,E)\), \(G\) is acyclic if and only if there exists \(f:V \rightarrow [n]\) s.t. \(f(u) \lt f(v)\) for every \(\overrightarrow{u v}\).
If direction: Suppose that (a) there is such \(f\) but (b) \(G\) has cycle \((v_0,v_1,\ldots,v_k)\)
Then \(f(v_0) \lt f(v_1) \lt \cdots \lt f(v_k) \lt f(v_0)\)!
Only if direction: Suppose that \(G\) acyclic.
Claim: \(G\) has “sink”: vertex \(s\) with out-degree zero.
Proof: Start walking from some vertex \(v\) until we get stuck.
Idea for sorting: Set \(f(s)=n\) for sink \(s\), remove \(s\) from graph, continue.
Full proof (1)
Disclaimer: Limit to formality / verbosity in slides.
Lemma 1: Every DAG has a sink
Proof: Suppose, towards sake of contradiction, that \(G=(V,E)\), with \(n=|v|\) has no cycles and no sink.
Pick \(u_0\in V\), and pick \(u_1\) s.t. \(\overrightarrow{u_0 u_1}\). (Must exist since \(u_0\) is not sink)
Pick \(u_2\) s.t. \(\overrightarrow{u_1 u_2}\) , \(u_3\) s.t. \(\overrightarrow{u_2 u_3}\) , and continue with \(u_i\) satisfying \(\overrightarrow{u_{i-1} u_i}\) for \(i=0,1,\ldots,n\)
Among \(u_0,u_1,\ldots,u_n\) there must be \(i \neq j\) such that \(u_i=u_j\). (Can’t have \(n+1\) distinct members of an \(n\) sized set \(V\).)
w.l.o.g \(i \lt j\).
But then \((u_i,u_{i+1},u_{i+2},\ldots,u_{j-1},u_j)\) is a cycle: a contradiction! QED
Full proof (2)
Topological Sort Thm: For every \(n\)-vertex directed \(G=(V,E)\), \(G\) is acyclic if and only if there exists \(f:V \rightarrow [n]\) s.t. \(f(u) \lt f(v)\) for every \(\overrightarrow{u v}\).
Proof: Let \(G=(V,E)\) be DAG. Induction on \(n=|V|\). (\(n=1\): trivial)
Let \(s\) sink (via Lemma 1), \(G'=(V',E')\) obtained by removing \(s\)
(\(G'\) is DAG: removing can’t create cycles)
By inductive hyp., \(\exists f':V' \rightarrow [n-1]\) s.t. \(\color{red}{f'(u) \lt f'(v)}\) for every \(\overrightarrow{u v} \in E'\). Define:
For every \(\overrightarrow{u v} \in E\), if \(u,v \neq s\) then \(f(u)= f'(u) \lt f'(v)=f(v)\).
Otherwise \(v=s\) (sink can’t be \(u\)) and \(f(u) = f'(u) \lt f(v)= f(s)=n\). QED
Proofs and programs
- Understand the question
- Get high level idea how to solve it
- Work out outline on napkin / pad / whiteboard
- Write down plugging all gaps
“Debugging” proofs:
- Type safety: If proofs refers to \(x\), what is it? where did it come from? what do we know about it? why can we assume it exists?
- Scope: For every sentence/equation, what argument does it belong to? Is it part of a proof of an intermediate claim? is this a fact established from the previous arguments? Is this a new claim that will need to be proved?
Cargo Cult Proofs

Cargo Cult Science, Richard Feynmann, 1974
Cargo Cult Proofs
A proof is not about the ritual, symbols, rules, conventions.

A proof is an air-tight argument that the statement is true.
Conventions are designed to help ensure this.
Functions and pigeons
Function
One to one (injective) functions
Onto (surjective) functions
Functions and cardinalities
Thm: For every finite sets \(S,T\), the following are equivalent:
1. \(|S| \leq |T|\)
2. There exists one to one \(f:S \rightarrow T\).
3. There exists onto \(g:T \rightarrow S\)
Corollary: \(|S|=|T|\) iff there is a bijection \(f:S \rightarrow T\)
3 minutes: Convince your neighbor that corollary follows from theorem
Functions and cardinalities
Thm: For every finite sets \(S,T\), the following are equivalent:
1. \(|S| \leq |T|\)
2. There exists one to one \(f:S \rightarrow T\).
3. There exists onto \(g:T \rightarrow S\)
Proof:
\(\color{red}{1 \Rightarrow 2:}\) Write \(S=\{ s_0,\ldots, s_{k-1} \}\), \(T = \{ t_0,\ldots, t_{m-1} \}\). Define \(f(s_i)=t_i\).
Functions and cardinalities
Thm: For every finite sets \(S,T\), the following are equivalent:
1. \(|S| \leq |T|\)
2. There exists one to one \(f:S \rightarrow T\).
3. There exists onto \(g:T \rightarrow S\)
Proof:
\(\color{red}{2 \Rightarrow 3:}\) Let \(f:S \rightarrow T\) one to one. Define \(g(t)\) be \(s\) s.t. \(f(s)=t\), otherwise \(g(t)=s_0\).
Functions and cardinalities
Thm: For every finite sets \(S,T\), the following are equivalent:
1. \(|S| \leq |T|\)
2. There exists one to one \(f:S \rightarrow T\).
3. There exists onto \(g:T \rightarrow S\)
Proof:
\(\color{red}{3 \Rightarrow 1:}\) Let \(g:T \rightarrow S\) be onto. Write \(T = \{ t_0, t_1,\ldots, t_{m-1} \}\). Then \(S = \{ g(t_0), g(t_1),\ldots, g(t_{m-1}) \}\). \(|S|=|\{ g(t_0),g(t_1),\ldots, g(t_{m-1}) \}| \leq |m|\)
Trickier for infinite sets
Thm: (“Hilbert’s Hotel”) There is a one-to-one function from \(\mathbb{N}\) to \(\mathbb{N}\setminus \{ 0 \}\).
Proof:..
Trickier for infinite sets
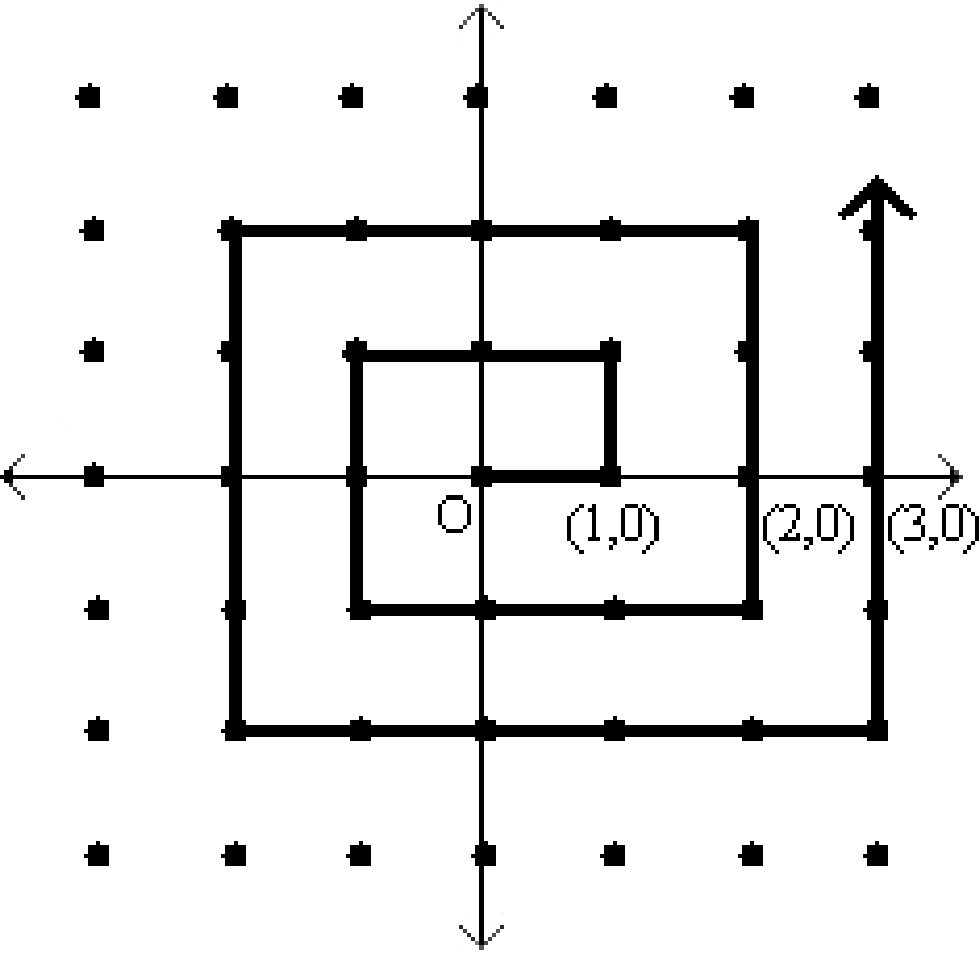
Thm: There is one-to-one function \(f:\mathbb{Z}^2 \rightarrow \mathbb{N}\).
Proof:..
Number of functions
Thm: \(|\{ f \;|\; f: A \rightarrow B \}| = |B|^{|A|}\)
Proof: Write \(A = \{ a_0,a_1,\ldots, a_{m-1} \}\) and \(B=\{ b_0,\ldots, b_{k-1} \}\).
To specify \(f: A \rightarrow B\), make \(k\) choices for \(f(a_0)\), make \(k\) choices for \(f(a_1)\), etc..
Back to graphs
Theorem (Green-Tao 2003): There exist numbers \(p,a\in \mathbb{N}\) s.t.
\[ p, p+a, p+2a, \ldots, p+100a \]are all prime numbers.
One component of proof: Expert learning / Boosting /Linear programming duality / Min max theorem /Hahn Banach Theorem / Hardcore Lemma / Dense model theorem
General theme:
A large enough object will contain arbitrary structure.
The most “structureless” object is a random object.
“Ramsey Theory”
Another instance


Bible codes
Doron Witztum, Eliyahu Rips, and Yoav Rosenberg, “Equidistant Letter Sequences in the Book of Genesis”, Statistical Science Volume 9, Number 3 (1994), 429-438.
“(In) Book of Genesis … equidistant letter sequences spelling words with related meanings often appear in close proximity. … effect is significant at the level of 0.00002.”
Maya Bar-Hillel, Dror Bar-Natan, Gil Kalai, and Brendan McKay, “Solving the Bible Code Puzzle”, Statistical Science Volume 14, Number 2 (1999), 150-173.
We … produce an equally small significance level using the text of Tolstoy’s War and Peace instead of the text of Genesis
A large enough object will contain arbitrary structure.
Mother of all Ramsey results
Theorem (Ramsey 1930): Every graph on \(n\) vertices contains either a clique or independent set of \(\geq \tfrac{\lfloor \log n \rfloor}{2}\) vertices.
Step 1: Understand what the statement means:
Clique: A subset \(S\) of vertices s.t. \(u \sim v\) for every \(u\neq v \in S\).
Independent set: A subset \(S\) of vertices s.t. \(u \not\sim v\) for every \(u\neq v \in S\).
A priori: Maybe can find \(100\) vertex graph \(G\) such that (1) \(G\) contains no triangles, but (2) every three vertices \(\{u,v,w \} \subseteq V(G)\) contain one edge.
No: In every group of six people, either there are three who don’t know each other, or three that are mutual acquaintances.
Mother of all Ramsey results
Theorem (Ramsey 1928): Every graph on \(n\) vertices contains either a clique or independent set of \(\geq \tfrac{\lfloor \log n \rfloor}{2}\) vertices.
Step 2: Convince yourself that statement is true.
Break into pairs to prove: Every graph of \(256=2^8\) vertices contains either a \(4\)-clique or \(4\) independent set.
Mother of all Ramsey results
Theorem (Ramsey 1928): Every graph on \(n\) vertices contains either a clique or independent set of \(\geq \tfrac{\lfloor \log n \rfloor}{2}\) vertices.
Proof: Let \(G=G(V,E)\) be any \(n\) vertex graph. Let \(S_0=V\) and for \(i=0,1,\ldots,\lfloor \log n \rfloor\) do:
- Pick some \(v_i \in S_i\).
- If \(|\Gamma(v_i) \cap S_i| \geq |S_i|/2\) call \(v_i\) “blue” and let \(S_{i+1} = S_i \cap \Gamma(v_i)\). Otherwise call \(v_i\) “red” and let \(S_{i+1} = S_i \setminus \Gamma(v_i)\)
- Let \(i=i+1\).
Claim 1: For every \(i\in \{0,\ldots,\lfloor\log n/2\rfloor\}\), \(S_{i+1} \subseteq S_i\), \(|S_{i+1}| \geq |S_i|/2\).
Proof: We choose \(S_{i+1}\) to be a subset of \(S_i\) with at least half its vertices.
Corollary: \(S_i\) will never be empty.
Proof: \(|S_i| \geq n/2^i\).
Claim 2: The blue vertices are a clique.
Example: Suppose sequence is \(\color{red}{v_0}, \color{cyan}{v_1}, \color{cyan}{v_2},\color{red}{v_3},\color{cyan}{v_4}\).
\(v_2 \in S_2 \subseteq \Gamma(v_1)\) \(\color{orange}{\Rightarrow}\) \(v_2 \sim v_1\) , \(v_4 \in S_4 \subseteq \Gamma(v_1) \cap \Gamma(v_2)\) \(\color{orange}{\Rightarrow}\) \(v_4 \sim v_2\), \(v_4 \sim v_1\)
Conclusion: \(\{ \color{cyan}{v_1},\color{cyan}{v_2}, \color{cyan}{v_4} \}\) are a clique.
Mother of all Ramsey results
Theorem (Ramsey 1928): Every graph on \(n\) vertices contains either a clique or independent set of \(\geq \tfrac{\lfloor \log n \rfloor}{2}\) vertices.
Proof: Let \(G=G(V,E)\) be any \(n\) vertex graph. Let \(S_0=V\) and for \(i=0,1,\ldots,\lfloor \log n \rfloor\) do:
- Pick some \(v_i \in S_i\).
- If \(|\Gamma(v_i) \cap S_i| \geq |S_i|/2\) call \(v_i\) “blue” and let \(S_{i+1} = S_i \cap \Gamma(v_i)\). Otherwise call \(v_i\) “red” and let \(S_{i+1} = S_i \setminus \Gamma(v_i)\)
- Let \(i=i+1\).
Claim 1: For every \(i\in \{0,\ldots,\lfloor\log n/2\rfloor\}\), \(S_{i+1} \subseteq S_i\), \(|S_{i+1}| \geq |S_i|/2\).
Claim 2: The blue vertices are a clique and the red vertices are independent set
Proof: Let \(\color{cyan}{v_{i_1}},\ldots,\color{cyan}{v_{i_k}}\) be the blue vertices with \(i_1 \lt i_2 \lt \ldots \lt i_k\). Then For every \(j \lt j' \in \{1,\ldots,k\}\), \(v_{i_{j'}} \in S_{i_{j'}} \subseteq S_{i_j+1} \subseteq \Gamma(v_{i_j})\) and hence \(v_{i_j} \sim v_{i_{j'}}\).
The red case is proved analogously.
Corollary: \(\exists\) either clique or independent set of \(\geq \lfloor \log n \rfloor/2\) vertices.
Mother of all Ramsey results
Theorem (Ramsey 1928): Every graph on \(n\) vertices contains either a clique or independent set of \(\geq \tfrac{\lfloor \log n \rfloor}{2}\) vertices.
Theorem (Erdős 1947): With high probability, a random graph on \(n\) vertices will contain neither a clique nor an independent set of more than \(2.001 \log n\) vertices.
Questions:
- What is the right bound?
- Can we find a deterministic construction?
- Best known: Improve Ramsey’s Thm to (less than) \(0.500001 \log n\) vertices. (…, Conlon, Annals of Math, 2009)
- Best deterministic construction is graph with smallest set of about \((\log n)^{100}\) vertices (…,Chattopadhyay- Zuckerman 2016, Cohen 2017)
Related to questions such as extracting randomness from entropy sources.
What’s next?
Covered some math, we’ll pick up more when we need.
Next up: What do we want to compute: representing inputs, outputs, computational tasks.
After that: How do we compute: modeling computational processes.