N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 3: Representing objects as strings
Boaz Barak (instructor), Salil Vadhan (co-instructor), Juan Perdomo (Head TF).
Team: Aditya Mahadevan, Brian Sapozhnikov (surveys), Chan Kang (extension), Gabe Abrams (Ed Tech), Gabe Montague (NAND web), Jessica Zhu (proof workshops), John Shen, Juan Esteller (NAND implementation), Karl Otness, Katherine Binnery, Lisa Lu, Mark Goldstein, Stefan Spataru, Susan Xu, Tara Sowrirajan, Thomas Orton (Advanced Section), Wentong Zhang
Slides will be posted online.

Laptops/phones only on last 3 rows please.


“Digital representations have been catalyzed by computers, but they are fundamentally about the symbols, not the technology that records them, and they were with us long before any of our current electronic devices.”
“With the discovery that a cell’s protein content is encoded using three-letter words written in an alphabet of four genetic bases, the field of biology stumbled upon an ancient digital representation of remarkable sophistication and power.”
What is computation?
One definition: Mapping input to output.
“Axiom:” All our inputs and outputs can be encoded as binary strings of finite length.
“Algorithm \(A\) multiplies two numbers” is really
“Given the encoding of \(x\) and \(y\), \(A(x,y)\) outputs the encoding of \(x\times y\)”
Representation and Computation
Choosing representation makes a difference
- Compression: representation with small size (e.g., JPEG)
- Error correction: representation that is robust to errors (e.g., “control digits”, error correcting codes)
- Data structures: representation enabling fast operations (e.g., binary numbers, distance oracles)
- Feature extraction: representation enabling prediction (e.g., deep nets)
- Secrecy: representation hiding certain information (e.g., encryption, commitment)
Our focus: Some representation of objects as strings.
What is “the number \(17\)”?
- \(17\)
- XVII
- \((1,0,0,0,1)\)
- 0x11
The “thing outside the cave” whose shadows are the above?
Doesn’t matter?
Definition of representation:
Set \(\mathscr{O}\) of objects
Examples:
- Numbers
- Text
- Images
- MRI scans
- Matrices
- Graphs
- Computer programs
- …
Definition of representation:
A representation of \(\mathscr{O}\) as \(\mathscr{R}\) (usually \(\mathscr{R}=\{0,1\}^*\)) consists of:
Encoding function \(E:\mathscr{O} \rightarrow \mathscr{R}\) which is one-to-one.
Decoding function \(D:\mathscr{R} \rightarrow \mathscr{O}\) which is onto.
\(E,D\) satisfy \(\color{red}{(*)}\): \(D(E(o))=o\) for every \(o\in\mathscr{O}\).
Example 1: Representing natural numbers via binary basis:
- \(D(x_0,\ldots,x_{n-1})=x_0 + x_1\cdot 2^1 +\cdots + x_{n-1}\cdot 2^{n-1}\).
- \(E(o) = (x_0,\ldots, x_{n-1})\) s.t. \(x_i = \lfloor \tfrac{x}{2^i} \rfloor \mod 2\) for \(i \in [n]\).
Example 2: Represent graphs as adjacency matrix
Example 3: Represent English text as ASCII or UTF-8 strings
Definition of representation:
A representation of \(\mathscr{O}\) as \(\mathscr{R}\) (usually \(\mathscr{R}=\{0,1\}^*\)) consists of:
- Encoding function \(E:\mathscr{O} \rightarrow \mathscr{R}\) which is 1-to-1.
Decoding function \(D:\mathscr{R} \rightarrow \mathscr{O}\) which is onto.
\(E,D\) satisfy \(\color{red}{(*)}\): \(D(E(o))=o\) for every \(o\in\mathscr{O}\).
Definition of representation:
A representation of \(\mathscr{O}\) as \(\mathscr{R}\) (usually \(\mathscr{R}=\{0,1\}^*\)) consists of:
1. Encoding function \(E:\mathscr{O} \rightarrow \mathscr{R}\) which is 1-to-1.
2. Decoding function \(D:\mathscr{R} \rightarrow \mathscr{O}\) which is onto.
3. \(E,D\) satisfy \(\color{red}{(*)}\): \(D(E(o))=o\) for every \(o\in\mathscr{O}\).
All three conditions equivalent to existence of representation:
Lemma 1: If exists 1-1 \(E:\mathscr{O} \rightarrow \mathscr{R}\) then exists onto \(D:\mathscr{R} \rightarrow \mathscr{O}\) satisfying \(\color{red}{(*)}\).
Lemma 2: If there exists (even partial) onto \(D:\mathscr{R} \rightarrow \mathscr{O}\) then exists 1-to-1 \(E:\mathscr{O} \rightarrow \mathscr{R}\) satisfying \(\color{red}{(*)}\).
Lemma 3: If \(E:\mathscr{O} \rightarrow \mathscr{R}\), \(D:\mathscr{R} \rightarrow \mathscr{O}\) satisfy \(\color{red}{(*)}\) then \(E\) is 1-to-1 and \(D\) is onto.
Bottom line: Exists representation of \(\mathscr{O}\) as \(\mathscr{R}\) iff \(|\mathscr{O}|\leq |\mathscr{R}|\).
Transitivity of representation
Claim: If \(E: \mathscr{O} \rightarrow \mathscr{R}\) and \(F: \mathscr{R} \rightarrow \mathscr{S}\) are 1-to-1, then their composition \(F \circ E\) is 1-to-1.
Proof: If \(x \neq x'\) then \(E(x) \neq E(x')\) (since \(F\) is 1-to-1) and then \(F(E(x)) \neq F(E(x'))\) (since \(F\) is 1-to-1) ∎.
Corollary: If we can represent objects in \(\mathscr{O}\) as objects in \(\mathscr{R}\), and can represent objects in \(\mathscr{R}\) as strings in \(\{0,1\}^*\), then can represent \(\mathscr{O}\) as strings.
Example: \(\mathscr{O}\) = Python programs. \(\mathscr{R}\) = English text.
Corollary: Can represent Python programs as strings.
Prefix freeness
Def: Representation \(E:\mathscr{O} \rightarrow \{0,1\}^*\) is prefix free if there are no \(o\neq o'\) such that for every \(i \in [|E(o)|]\), \(E(o)_i = E(o')_i\).
English is not prefix free: teacher stalking.com
Prefix free encoding of English words: use spaces sentences (list of words) : use spaces and periods
Prefix freeness
Def: Representation \(E:\mathscr{O} \rightarrow \{0,1\}^*\) is prefix free if there are no \(o\neq o'\) such that for every \(i \in [|E(o)|]\), \(E(o)_i = E(o')_i\).
Examples:
- Binary representation of \({\mathbb{N}}\) to \(\{0,1\}^*\).
- Binary representation of \([1000]\) to \(\{0,1\}^{10}\) with leading zeroes.
- UTF-8 representation of symbols.
- concatenated UTF-8 representation of strings.
Making every representation prefix free
- Modify \(E:\mathscr{O} \rightarrow \{0,1\}^*\) to prefix-free \(E:\mathscr{O} \rightarrow \{0,1,;\}^*\)
- Compose with representation \(E':\{0,1,;\} \rightarrow \{ 0,1 \}^2\)
Cost: \(n \mapsto 2n+2\).
Solutions with \(n + O(\log n)\), even \(n + \log n + O(\log \log n)\).
No solution with \(n + 0.99\log n\) (see Kraft’s Inequality exercise in notes!)
Huffman codes: Prefix free encodings with minimum average length.
Encoding strings
- “C Style” - null terminated string: Represent \(s_0,\ldots,s_{n-1} \in \{1,\ldots,255 \}\) as \((s_0,s_1,\ldots,s_{n-1},0)\)
Easy code to copy: while (*buffer++ = *str++) ;
- “Pascal style” - length-prefix string: Represent \(s_0,\ldots,s_{n-1}\in \{0,\ldots,255 \}\) with \(n \leq 255\) as \((n,s_0,\ldots,s_{n-1})\) (variants with more bytes: \(4\) bytes suffices for \(2^{32}=1GB\) )
Quickly compute len(s)
Tradeoffs between memory use and efficiency of operations
Buffer overflows..
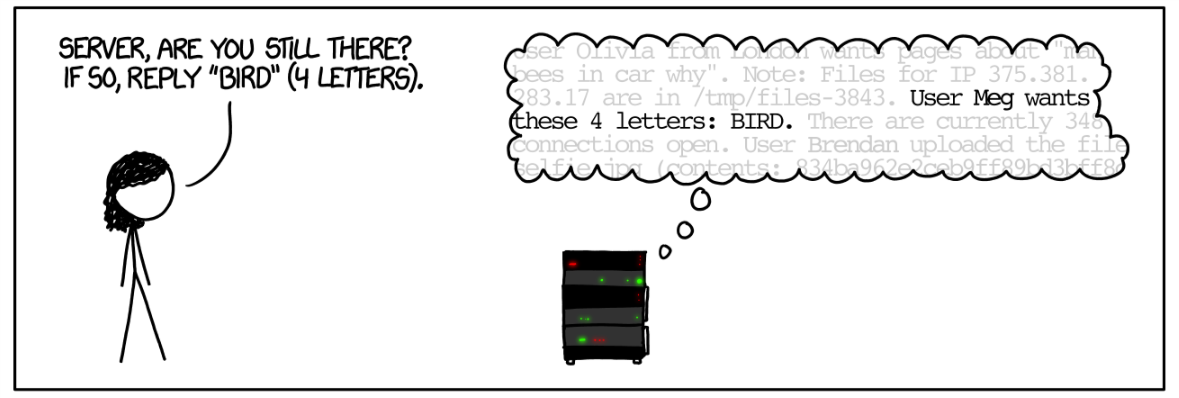
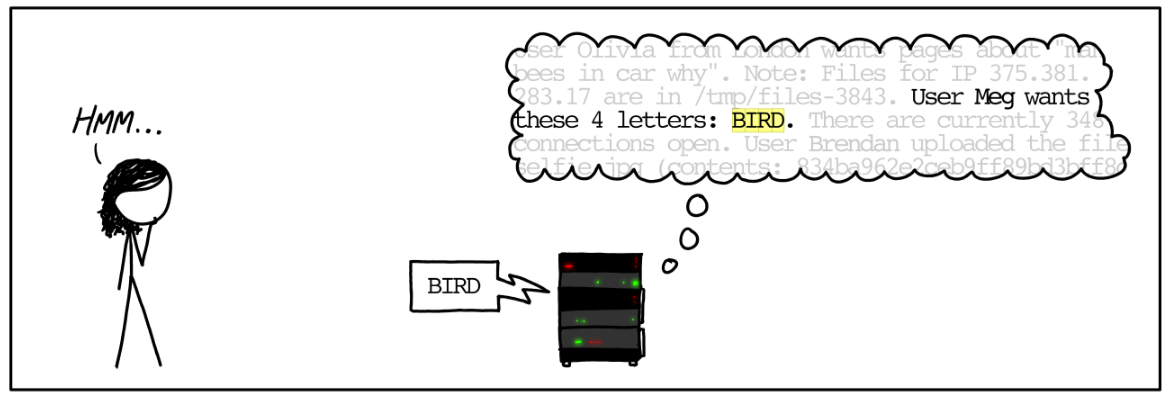
TLS Heartbeat protocol
Goal: Check connection with server, keep it alive
Client to Server: Send string \(s\)
Server to Client: Send \(s\) back
Concretely: \(s\) represented as \((payload,p)\), \(payload \in {\mathbb{N}}\), \(p \in \{0,1\}^*\), \(payload = |p|\).
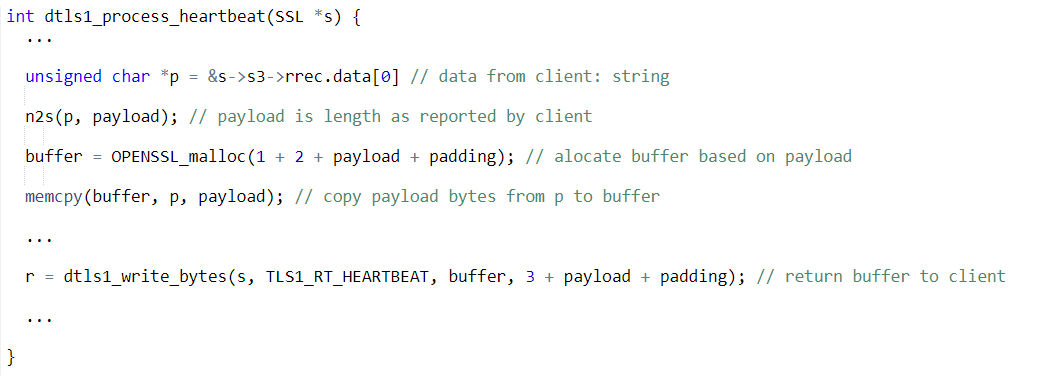
Heartbleed
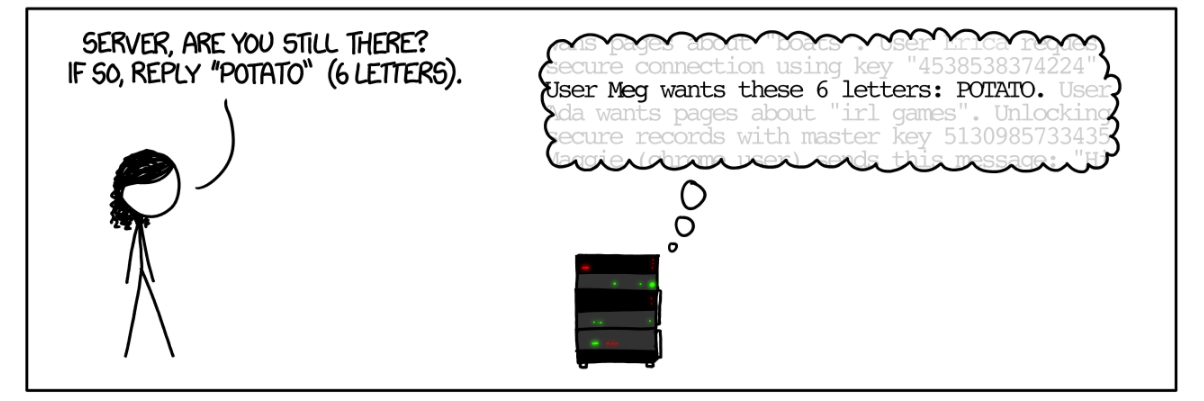
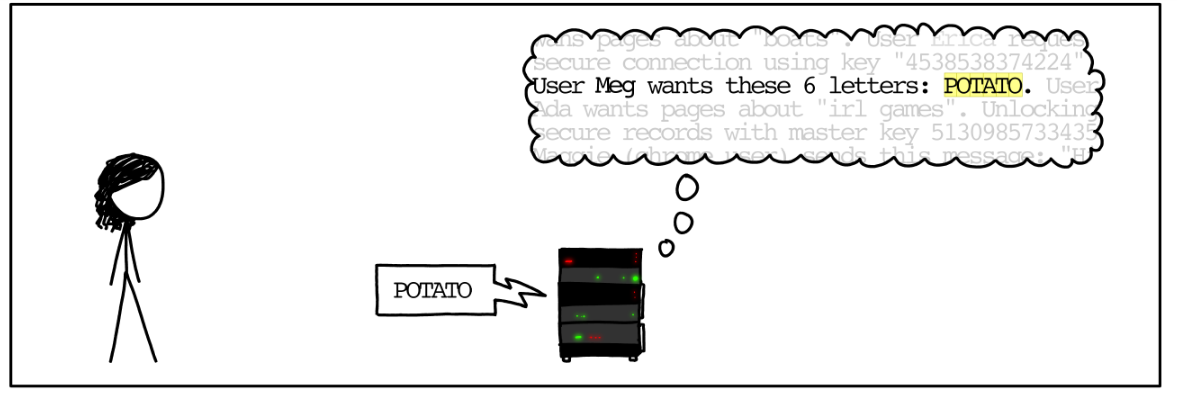
Heartbleed
Heartbleed
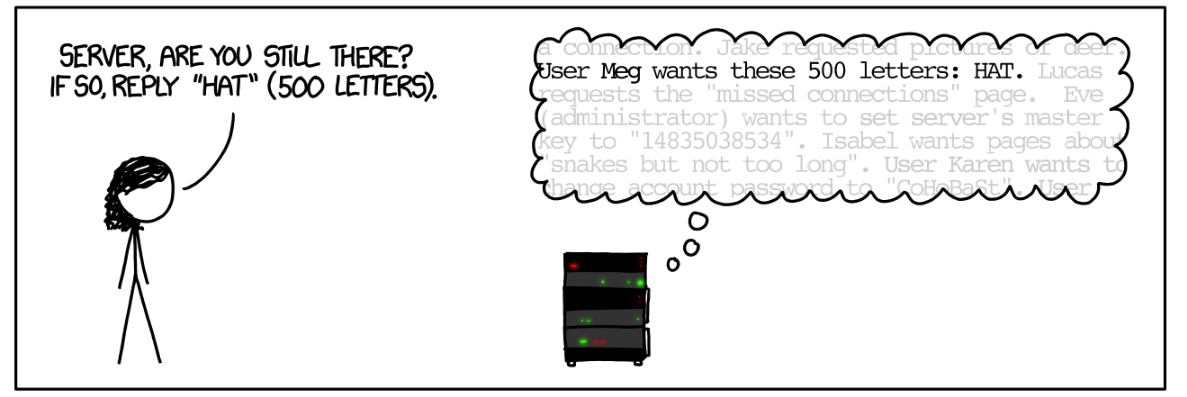
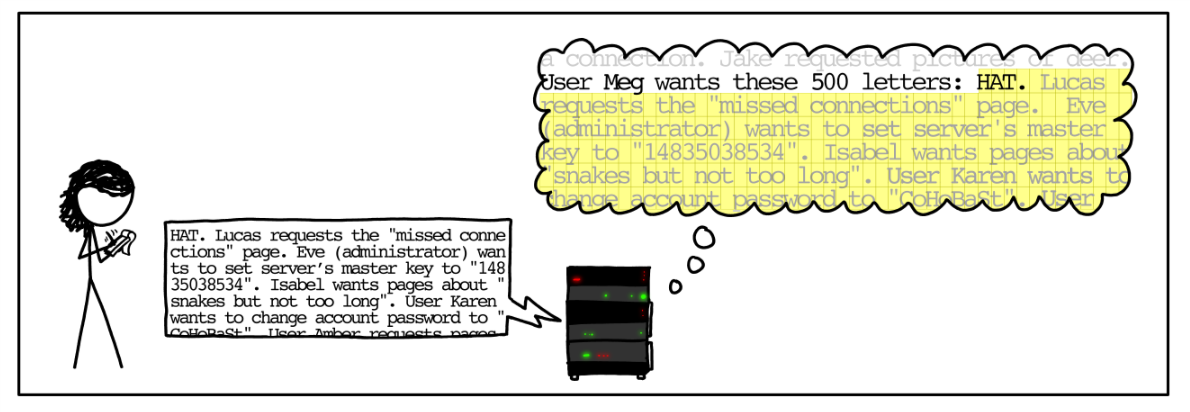
Heartbleed
“Some might argue that it is the worst vulnerability found (at least in terms of its potential impact) since commercial traffic began to flow on the Internet.”, Joseph Steinberg , Forbes.
Representing anything?
“Axiom”: Can represent anything as zeroes and ones.
What about real numbers? Say between \(0\) and \(1\)?
Represent \(3/8 = 1/4 + 1/8\) as \(0.011\) in binary.
What about \(1/10\)? Or \(1/3\)? Represent \(a/b\) as \((a,b)\).
What about \(1/\pi\)?
Unfortunate fact
Thm: (Cantor, 1874) No 1-to-1 map \(RtS:\mathbb{R} \rightarrow \{0,1\}^*\)
Lemma 1: Exists 1-to-1 map from \(FtR:\{0,1\}^\infty \rightarrow \mathbb{R}\)
(\(\{0,1\}^\infty = \{ f \;|\; f:{\mathbb{N}}\rightarrow \{0,1\} \}\))
Lemma 2: No onto map \(StF:\{0,1\}^* \rightarrow \{0,1\}^\infty\).
Lemma 1 + Lemma 2 implies thm:
Lemma 1: Exists 1-to-1 map from \(FtR:\{0,1\}^\infty \rightarrow \mathbb{R}\).
Proof: For every \(f \in \{0,1\}^\infty\) (i.e. \(f:{\mathbb{N}}\rightarrow \{0,1\}\)) define
One to one because \(f(i) \neq f'(i)\) implies \(|FtR(f)-FtR(f')| \gt \tfrac{8}{9} \cdot 10^{-i}\).
Lemma 2: No onto map \(StF:\{0,1\}^* \rightarrow \{0,1\}^\infty\).
Lemma 2’: No onto map \(NtF:{\mathbb{N}}\rightarrow \{0,1\}^\infty\).
Proof: Find \(f^* \in \{0,1\}^\infty\) s.t. \(f^* \neq NtF(n)\) for every \(n\)
That is, for every \(n\) there is \(m\) s.t. \(f^*(m) \neq NtF(n)(m)\).
Representing reals
Floating point: Given budgets \(k,\ell\), represent \(x\in \mathbb{R}\) as \((a,b) \in {\mathbb{Z}}^2\) with \(|a| \leq 2^k\), \(|b|\leq 2^\ell\) such that \(|x- a2^{b}|\) is minimal.
Cost: \(\sim\) \(2+k+\ell\) bits.
Accuracy: Can represent numbers in \([-2^k,+2^k]\) up to \(2^{k-\ell}\) error.
IEEE 754 double precision floating point (Javascript “number”, Python “float”, C “double”*: \(64\) bits: \(\sim\) \(k=53\), \(\ell=11\).
single precision: \(32\) bits: \(\sim\) \(k=24\), \(\ell=8\).
Rule of thumb: Avoid floats if you can. Money and time are not floats.
Representing reals
