N or Space for next slide, P for previous slide, F for full screen, M for menu

Lec 10:Other computational models

Boaz Barak (instructor), Salil Vadhan (co-instructor), Juan Perdomo (Head TF).

Team: Aditya Mahadevan, Brian Sapozhnikov (surveys), Chan Kang (extension), Gabe Abrams (Ed Tech), Gabe Montague (NAND web), Jessica Zhu (proof workshops), John Shen, Juan Esteller (NAND implementation), Karl Otness, Katherine Binney, Mark Goldstein (clicker expert), Stefan Spataru, Susan Xu, Tara Sowrirajan, Thomas Orton (Advanced Section)

http://tiny.cc/cs121

Slides will be posted online.


Laptops/phones only on last 3 rows please.

Announcements

  • Course resources

  • Calendar

  • Salil review lecture Tuesday 10/10 evening

  • Midterm prep questions

  • Main theorems

  • No pset before midterm

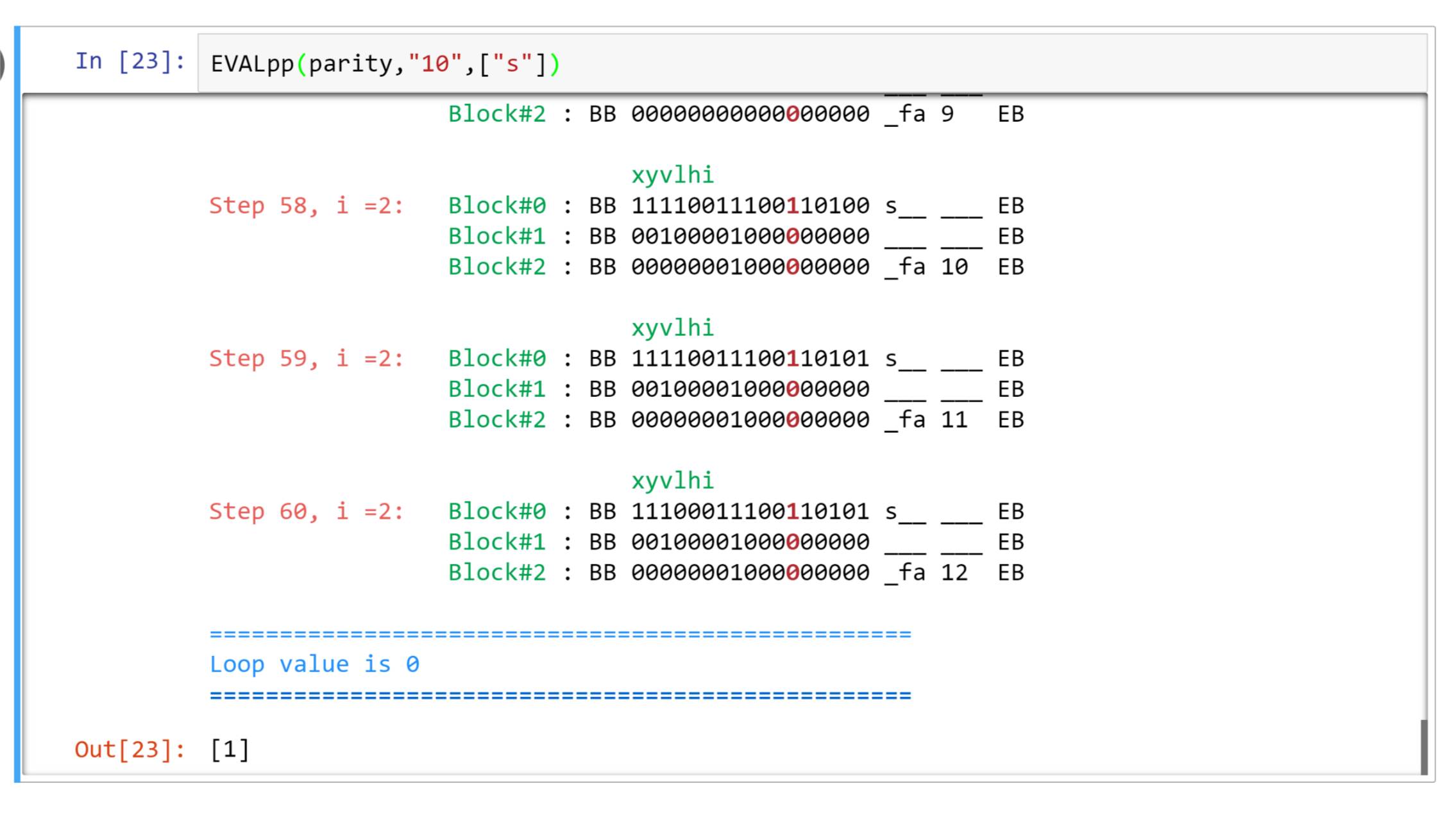
NAND++ configuration review

  • Think of variables as arrays

  • Config: seqeuence of blocks. Initially \(n\)*, eventually largest index reached \(i\).

  • Main point: Computation is sequence of simple operations.

Modeling computation

1930’s: Three different definitions of “computable functions”

  • \(\lambda\) calculus (Alonzo Church 1932,1936)

  • General recursive functions (Kurt Gödel 1934)

  • Turing machines (Alan Turing 1937)

Church: Conjectured “\(\lambda\) computable = computable”.

Gödel: Unconvinced. Proposes “general recursive”

Church+Kleene: Two definitions equivalent

Gödel: Maybe both equivalent but “wrong”

Turing: Defines “Turing machines” (shows equivalent to \(\lambda\) calculus)

Gödel, Church, everyone: Convinced captures computation

Question

What’s the corresponding element in a Turing machine to the NAND++ index variable i?

a. Current state

b. Alphabet size

c. Head position

d. State transition function

Turing machine

Models person with:

  • Unbounded sheet of paper (“tape”)

  • Finite working memory (“states”)

  • Each step: Read/Write one symbol, update memory, move to adjacent tape location.

Example: Person computing \(a \times b\) using gradeschool algorithm.

Question: Why did Turing try to model a person and not an electronic computer?

Today’s Lecture

NAND<< to NAND++ reduction 1

Features: integer variables | arithmetic operations | arithmetic with index

Question: How can we simulate integer arrays with two dimensional bit arrays?

NAND<< to NAND++ reduction 2

Features: Integer variables | 2-dim arrays | Arithmetic operations | Arithmetic with index

Question: How can we simulate two dimensional arrays with one dimensional arrays?

Answer: Replace the indices \((i,j)\) with \(PAIR(i,j)\) where \(PAIR:\mathbb{N}^2 \rightarrow \mathbb{N}\) is one-to-one (e.g., \(PAIR(x,y)=\tfrac{1}{2}(x+y+1)(x+y)+x\))

NAND<< to NAND++ reduction 3

Features: Integer variables | 2-dim arrays | Arithmetic operations | Arithmetic with index

Question: How can we implement arithmetic operations on bit-representations of integers?

Answer: Like we learned in school

NAND<< to NAND++ reduction 4

Features: Integer variables | 2-dim arrays | Arithmetic operations | Arithmetic with index

Question: How can we use \(i++\) and \(i--\) to implement COPYTOi(foo)

Answer:

  1. Array marker initially set to \((1,0,\ldots)\)

  2. Repeat: decrement foo and move \(1\) in marker one step right.

  3. Move \(i\) until we reach point where marker is equal to \(1\).

NAND<< to NAND++ reduction 4

Features: Integer variables | 2-dim arrays | Arithmetic operations | Arithmetic with index | Increment/decrement index

Question: How do we implement \(i++\) and \(i--\) in NAND++?

Answer: “Breadcrumbs” and “wait for bus strategy”

atstart_i initialized to \((1,0,0,0,\ldots)\)

breadcrumbs_i set to \(1\) at the end of every loop

indexincreasing set to \(1\) when at \(i=0\),set to \(0\) at new point.

marker usually all zeroes, set to \(1\) at a point we want to reach again.

Today’s Lecture

Turing machines

Def: A Turing Machine is \(M:[k] \times \Sigma \rightarrow [k] \times \Sigma \times \{L,R\}\)

\[(\text{new-state},\text{write},\text{dir})=M(\text{old-state},\text{read})\]









Question: Prove that two-way infinite tape is same as one-way infinite tape.

Two-tape TMs = One-tape TMs

Idea: Odd location tape 1, Even location tape 2.

Add “marker” for heads location: \(\Sigma \mapsto \Sigma \times \{ m,u \}\)

Simulate one step:

  1. Start in even location: go in jumps of two to find “even head” and read value.
  1. Move to odd, find “odd head” and read value
  1. Compute new state, vals to be written, directions.
  1. Scan to find heads and update.

New state: \([k] \mapsto [k] \times [k'] \approx [k\times k']\)

Main Thm

Thm: \(F\) NAND++-computable iff \(F\) TM-computable

Proof: \(\Leftarrow\): easy to simulate TM by NAND<<

\(\Rightarrow\): not hard to simulate NAND++ by TM. (head location = \(i\), state = line number + variables with absolute indices)

TM’s vs NAND++

Today’s Lecture

\(\lambda\) calculus

If \(f = \lambda x.e\) then \(f y\) is \(e[x \rightarrow y]\).

Currying \(\lambda x,y. exp = \lambda x.(\lambda y. exp)\)

Precedence rule: \(f x y = (f x) y\).

Question: Suppose that \(F = \lambda f. (\lambda x. (f x)f)\), \(1 = \lambda x.(\lambda y.x)\) and \(0=\lambda x.(\lambda y.y)\). What is \(F \; 1\; 0\)?

a. \(1\)

b. \(0\)

c. \(\lambda x.1\)

d. \(\lambda x.0\)

\(\lambda\)-computability

Informal: \(F\) is \(\lambda\)-computable if equal to \(\lambda\) expression.

Recall: \(NIL\) - empty list, \(PAIR\) - create pair. List \((a,b,c) = PAIR \; a \; (PAIR \; b \; (PAIR\; c \; NIL))\)

Formal: \(F:\{0,1\}^* \rightarrow \{0,1\}\) is \(\lambda\)-computable if exists \(\lambda\)-expression \(e\) such that for every \(x\in \{0,1\}^n\), \(F(x_0,\ldots,x_{n-1})\) equals

\[e PAIR \; x_0 (PAIR \; x_1 (cdots (PAIR \; x_{n-1} \; NIL))\cdots)\]

Thm: \(F\) is \(\lambda\)-computable iff \(F\) is NAND++ computable.

Proof: \(\Rightarrow\): repeat “search and replace” to evaluate \(\lambda\) expressions.

\(\Leftarrow\): crucial insight is \(NEXT_P\) is computable by “search and replace”

Preliminaries

  • Set \(0 = \lambda x,y.y\) and \(1= \lambda x,y.x\). Then \(IF \; cond \; a \; b = cond \; a \; b\).



  • Set \(PAIR = \lambda x,y. (\lambda f. f x y)\), \(HEAD = 1\), \(TAIL = 0\).



  • \(NIL = \lambda f.1\), \(ISNIL\; P = P (\lambda x,y.0)\).

To define \(MAP\), \(FILTER\), \(REDUCE\) we need recursion

Y combinator

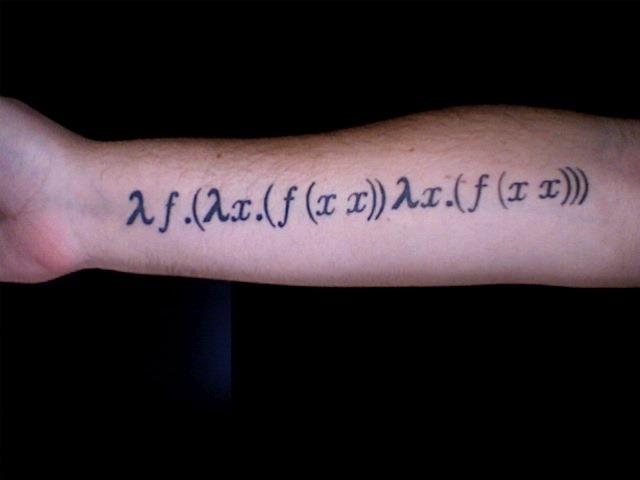
Turing Eret @turingmachine Hat-tip: Matt Might (see also Y combinator in Javascript)

Y combinator

Example:

\[PAR\; L = \begin{cases} 0 & ISNIL\;L \\ (HEAD\; L) \oplus (PAR\; (TAIL\; L)) & \text{o/w} \end{cases}\]

\[PAR\; L = (ISNIL\; L)\; 0 \;(XOR\; (HEAD\; L)\; (PAR\; (TAIL \;L)) \color{red}{(*)}\]

Question: Why is this a recursive definition for \(PAR\; L\)?

Non recursive function:

\[APAR \;\;\; = \lambda f,L. (ISNIL \; L)\; 0 \; (XOR \; (HEAD \; L) \; (f \; f \; (TAIL \; L)) \color{green}{(**)}\]

Lemma: \(PAR = APAR \; APAR\) satisfies equation \(\color{red}{(*)}\)

Proof: Plug \(f=APAR\) in \(\color{green}{(**)}\).

Cor: \(PAR \; L\) is the parity of \(L\) for every list \(L\).

Y combinator

Thm: Let \(Y = \lambda f. (\lambda x. f (x\; x)) (\lambda y. f (y\; y))\). Then for every \(F\), \(f=YF\) solves the recursive/fixed-point equation \(f=F\; f\).

Pf: Write

\(Y\; F = \color{green}{(\lambda x. F (x\; x))} \color{red}{(\lambda y. F (y\; y))}\) =\(\color{green}{F (x\; x)}[x \rightarrow \color{red}{\lambda y.F(y \; y)}]\)

=\(\color{green}{F(}\color{red}{(\lambda y.F(y \; y))} \; \color{red}{(\lambda y.F(y \; y))} \color{green}{)}\)

=\(F(Y F)\)

Using this can define \(FILTER\),\(MAP\),\(REDUCE\), etc..

Simulate NAND++ with \(\lambda\)

  • Simulate \(NEXT_P\)

  • Recursively repeat until halt

  • Configuration: list of blocks

Crucial observations:

  1. \(\lambda\) can do AND/OR/NOT \(\Rightarrow\) any finite function
  1. Next configuration is obtained by finite function applied to finitely many blocks. \(\Rightarrow\) \(FILTER\) to find active block and then constantly many applications of \(MAP\)/\(REDUCE\)

Church-Turing Thesis

“Computable” \(\approx\) TM-computable

= \(\lambda\)-computable

= NAND++ computable

= NAND<< computable

= Python-computable

\(\approx\) “Human computable”

\(\approx\) “Alien computable”

= ….

Opps, you cannot play draw N guess with this browser!