\renewcommand{}{}
N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 15: Modeling Efficient computation
Boaz Barak (instructor), Salil Vadhan (co-instructor), Juan Perdomo (Head TF).
Team: Aditya Mahadevan, Brian Sapozhnikov (surveys), Chan Kang (extension), Gabe Abrams (Ed Tech), Gabe Montague (NAND web), Jessica Zhu (proof workshops), John Shen, Juan Esteller (NAND implementation), Karl Otness, Katherine Binney, Mark Goldstein (clicker expert), Stefan Spataru, Susan Xu, Tara Sowrirajan (mushroom forager), Thomas Orton (Advanced Section)
Slides will be posted online.

Laptops/phones only on last 3 rows please.
Announcements
- Quizzes (result not visible, reduced to 10% , increased bonus)
- Reading (Piazza posts with guidelines)
- This phase of the course
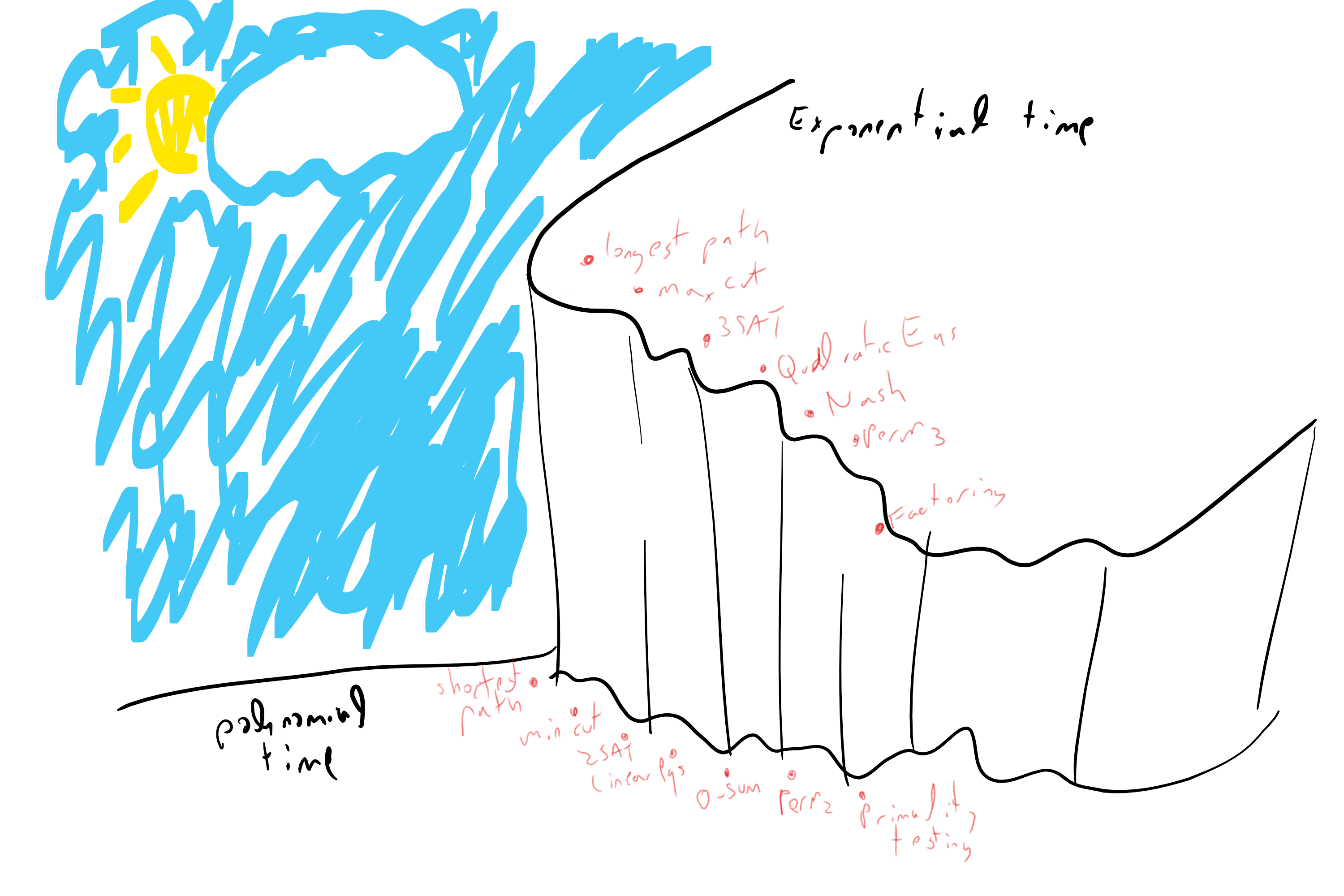
Modeling Running Time
Lesson No 1: Running time is function, not a number
\(T_P(n)\): largest (i.e., worst) number of steps a program \(P\) takes on inputs of length \(n\).
Examples: \(T(n)=100n\), \(T(n)=10\cdot n^2\), \(T(n)=2^n\), etc. etc.
Def: \(F: \{0,1\}^* \rightarrow \{0,1\}\) is in \(TIME(T(n))\) if there exists \(P\) s.t. for every large enough \(n\) and every \(x\in \{0,1\}^n\) , \(P\) halts within \(T(|x|)\) steps with output \(F(x)\).
Question 1: If we change exists to for every what would be the effect on set \(TIME(1000n)\)?
a) It would stay the same
b) It would become empty
c) It would contain every function from \(\{0,1\}^*\) to \(\{0,1\}\)
d) None of the above
Question 2: If we change every to there exists what would be the effect on set \(TIME(1000n)\)?
a) It would stay the same
b) It would become empty
c) It would contain every function from \(\{0,1\}^*\) to \(\{0,1\}\)
d) None of the above
Choosing the model
Lesson 2: At coarse enough resolution, model doesn’t matter.
Def of computable invariant under model: NAND++, NAND<< , RAM machines, Turing Machines, Cellular automata, \(\lambda\) calculus, Game of life, etc..
Def of \(TIME(T(n))\) is not invariant under model: exists \(F \in TIME_{\lt\lt}(100n)\) but \(F\not\in TIME_{++}(n^{1.1})\).
Q: Is there \(F \in TIME_{++}(100 n) \setminus TIME_{\lt\lt}(n^{1.1})\)? a) yes, b) no
Definition of \(\mathbf{P}\) and \(\mathbf{EXP}\) are invariant under model: NAND++, NAND<<, RAM machines, Turing machines, \(\lambda\) calculus*, etc… (Extended Church-Turing Thesis)
This course: mostly don’t care about difference of \(n^2\) vs \(n^5\).
In practice and other areas of theory: Care deeply. Use RAM models and more refined models and measures of resources: space, paralelism, communication, cache locality, …
Interlude: Nice functions
Def: \(T:\mathbb{N}\rightarrow \mathbb{N}\) is nice if \(T(n) \geq n\), \(T(n) \leq T(n+1)\) (more time for longer inputs) and \(T\) is itself in time \(T\) (program knows when to stop).
Q: Why include \(T(n) \geq n\) in requirements?
We only care about nice functions: \(n,n^2,1000n^3\log n,3^n\), etc..
\(NAND_{\lt\lt}\) vs \(NAND_{++}\)
Trivial: \(TIME_{++}(T(n)) \subseteq TIME_{\lt\lt}(T(n))\) for every \(T\).
Thm: There are constants \(a,b\) (less than \(10\)) s.t. \(TIME_{\lt\lt}(T(n)) \leq TIME_{++}(a T(n)^b)\)
Proof: Go back to proof that computability is same for both models, and count number of steps.
NAND<< to NAND++ reduction 1
Features: integer variables | arithmetic operations | arithmetic with index
Step 1: Simulate integer arrays with two dimensional bit arrays
Cost: \(O(bit size) = O(\log T)\) overhead: \(O(T)\) length integer array mapped to \(O(T \log T)\) length bit array
Step 2: Simulate two dimensional arrays with one dimensional arrays
Cost: Total memory stays the same \(O(T\log T)\) bits, \(polylog(T)\) overhead to compute index.
Step 3: Implement arithmetic operations on bit-representations of integers.
Cost: School algorithms: \(O(poly(\log T))\) overhead
NAND<< to NAND++ reduction 2
Step 4: Use \(i++\) and \(i--\) to move index to location in integer array foo
Approach: Shift marker and decrement foo until it is zero.
Cost: \(O(T^2)\)
Step 5: Implement \(i++\) and \(i--\) in NAND++?
Approach: “Breadcrumbs” and “wait for bus strategy”
Cost: Number of steps grows from \(T'\) to \(O(T'^2)\).
Total cost: \(O(T^4 poly(log T))\)
Bottom line
Up to poly overhead:
Extended Church Turing Thesis: True for all reasonable models.
Universal Machine: Pseudocode
Evaluating NAND<< programs in pseudocode:
- Maintain dictionary avars[name]=value
Do until avars[“loop”]=0 :
Execute every line var := expression: eval expression and update avars[var]
If expression contains index i then replace it with avars[“i”]
- Output avars[“y_0”]
If dictionary calls are \(O(1)\) then running time to simulate for \(T\) steps is \(O(T)\) steps.
Universal Machine: Python
Evaluating NAND<< programs in Python: (simplified)
def EVAL(P,x):
avars = { 'loop':0 }
while True:
for line in P.split('\n'):
(var,_,expr) := line.split(':=')
expr = expr.replace('_i',str(avars['i']))
avars[var] = EVALexpr(expr,avars)
if not avars['loop']: break
return avars['y_0']Universal Machine: NAND<<
Replace dictionary with array:
Map variable names into \([t]\)
\(j\)-th index of \(k\)-th variable is \(j\cdot t + k\).
One to one map \([t]\times \mathbb{N}\rightarrow \mathbb{N}\)
Thm: Can compute \(TIMEDEVAL(P,T,x)\) int time \(O(T)\). (\(O\) hides constants depending polynomially on \(|P|\).)
Cor: Universal Interview Answer
Cor: Universal Interview Answer
Q: Write an \(O(n\log n)\) program to do task “blah”
A: Enumerate over all programs and test each one
from itertools import product
import string
def BLAH(x):
n = 1
while True:
# iterate over all length n programs
symbols = string.ascii_letters+string.digits+" \n+-*/=(){},''"
for program in product(symbols, repeat=n):
y = eval(''.join(program),x) # eval prog on x
if TESTBLAH(x,y): return y
n += 1If there exists \(C\) character program solving BLAH in \(T(n)\) time, and running time to test Blah is \(Q(n)\), then running time is \(O(2^C(T(n)+Q(n)))\).
Time hierarchy theorem
Thm: For every nice \(T:\mathbb{N}\rightarrow \mathbb{N}\), \(TIME(T(n) \log n) \nsubseteq TIME(T(n))\)
note: Can replace \(\log n\) with any nice function \(f(n)\) going to infinity.
Pf: Bounded Halting function \(HALT_T\) designed so that:
(i) \(HALT_T \not\in TIME(T(n))\)
(ii) \(HALT_T \in TIME(T(n)\log n)\)
\(HALT_T(P,x) = 1\) iff \(|P| \leq \log\log |x|\) and \(M(x)=1\) within \(T(n)\sqrt{\log n}\) steps.
(i) follows immediately from \(TIMEDEVAL \in TIME(poly(|P|)T)\)
Proving time hierarchy thm
\(HALT_T(P,x) = 1\) iff \(|P| \leq \log\log |x|\) and \(M(x)=1\) within \(T(n)\sqrt{\log n}\) steps.
Lemma: \(HALT_T \not\in TIME(T(n))\)
Pf: Suppose \(H\) solves \(HALT_T\) in \(T(n)\) steps.
Program \(D(x)\):
1) If \(x\) not of form \(P10^k\) then loop
2) If \(H(P,P10^k)=1\) then loop
Let \(k\gt2^{2^{|D|}}\) then (i) \(HALT_T(D,D10^k) \neq 1\) (ii) \(HALT_T(D,D10^k) \neq 0\) contradiction!!
Pf of (i) Otherwise \(H(D,D10^k)=HALT_T(D,D10^k)=1\) and then \(D(D10^k)\) loops and \(HALT_T(D,D10^k)=0\).
Pf of (ii) Otherwise \(H(D,D10^k)=HALT_T(D,D10^k)=0\) and then \(D\) takes time \(O(n)\) for step 1 and \(T(n)\) for step 2, with total of \(O(T(n)) \ll T(n)\sqrt{\log n}\). Hence \(HALT_T(D,D10^k)=1\)
Asymptotic Analysis
- Abstract away implementation detail.
Focus on scaling behavior:
- \(O(n)\) time: doubling the input size doubles the time. \(c(2n)=2cn\)
- \(O(n^2)\) time: doubling the input size quadruples the time. \(c(2n)^2=4cn\)
- \(2^n\) time: adding one to the input doubles the time. \(2^{n+1}=2 \cdot 2^n\) doubling the input squares the time \(2^{2n}=(2^n)^2\)
Asymptotics and practice
- Constants matter, especially in exponents
- Refined measures matter (space, communication, caches)
- Moore’s law doesn’t help: inputs grow with cycles as technlogy improvements
- \(O(n)\) and \(O(n \log n)\) time algorithms executed in practice on petabyte size inputs (\(10^{15}\) bytes).
- A \(2^n\) algorithm is beyond even nation-states for \(16\) bytes input (breaking AES-128).
Definitions
\(TIME(O(n)) = \cup_c TIME(c n)\)
\(\mathbf{P} = TIME(poly(n)) = \cup_{c} TIME(n^c)\)
\(\mathbf{EXP} = TIME(2^{poly(n)}) = \cup_c TIME(2^{n^c})\)
\(\mathbf{P}\), \(\mathbf{EXP}\) invariant under NAND++, NAND<< , TMs, RAM machines, ..
NAND vs NAND<< vs NAND++
Thm: If \(F \in TIME(T(n))\) then for every large enough \(n\), \(F_n \in SIZE(10 T(n))\). \(F_n\) is \(F\) restricted to \(\{0,1\}^n\)
Proof by Python:
def index(k):
r = math.floor(math.sqrt(k+1/4)-1/2)
return (k-r*(r+1) if k <= (r+1)*(r+1) else (r+1)*(r+2)-k)
def NANDppTONAND(P,n,T):
res = ""
for t in range(T):
i = index(t)
valid = ('one' if i < n else 'zero' )
res += P.replace('validx_i',valid).replace('_i',str(i))
return rescode not 100% correct
