CS 121 / CSCI E121: Introduction to Theoretical Computer Science
Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow), Yueqi Sheng (Advanced section), Chi Ning Chou (Advanced section).

Laptops/phones only on last 5 rows please.
Put course in your Crimson Cart!
Which of these is a computer?
PollEv.com/cs121
a. 
c. 
b. 
d. 
e. All of the above.
Answer
All of the above .. but some have other uses as well

Slime mold as a computer
Integer multiplication
Input: Integers \(a,b\)
Output: \(a\times b\)
Iterated addition algorithm: Add \(a\) to itself \(b\) times.
(Using the deep fact \(a \times b = a + a + \cdots + a\) (\(b\) times))
Babylonian / grade-school algorithm: For \(i\),\(j\), add \(10^{i+j}a_ib_j\) to result.
Efficiency


Goren is a 1st grader that takes 30 seconds to multiply single-digit numbers.
The Summit is world’s fastest supercomputer, can do \(10^{17}\) floating points operations per second.
Q: Goren uses Babylonian and The Summit uses Iterated addition to multiply two \(80\) digit numbers. Who will finish first? (PollEv.com/cs121)
Analysis
Goren will take about \(80\times 80 \times 30 = 192,000\) seconds \(\approx\) \(53\) hours.
The Summit will take about \(10^{80} \approx 2^{256}\) additions.
How much is \(2^{256}\) operations?
Takeaway message
Algorithms matter more than technology.
(of course technology matters a lot too!)
This course: Study algorithms independently of technology.
Our main tool: Math
What is CS 121 about?
- Are there problems we can never solve?
- Are there mathematical theorems we can never prove?
- Can we always find a faster algorithm for a problem? Are there some problems where \(2^{256}\) is the best we can do?
- Can hardness be sometimes a good thing? Can we use it to make an unbreakable code? electronic cash?
- Can tossing random coins make computation faster?
- Can quantum entanglement make computation faster?
- Can we analyze how algorithms interact with people and data?
- Are there tradeoffs of efficiency vs. statistical accuracy? vs. incentive compatibility? vs. privacy?
- Can computation help unify gravity with quantum mechanics by explaining black holes?
Story of an algorithm
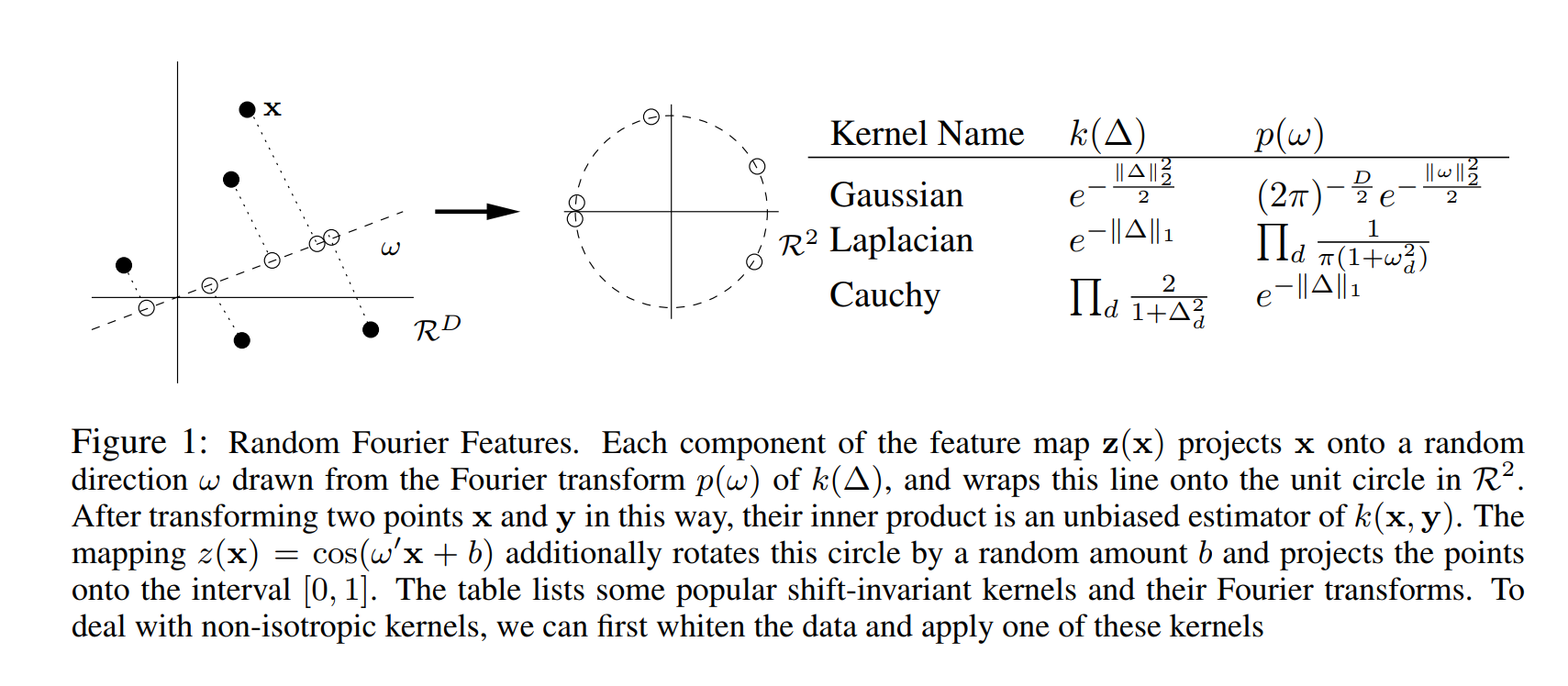
Fourier Transform
In 1822 Joseph Fourier proposed solution to “heat equation” using following observation:
Every (“nice”) \(f:[0,1] \rightarrow \mathbb{R}\) can be decomposed as a sum of wave functions of the form \(g(x) = \sin(a x)\) or \(g(x)=\cos(b x)\).

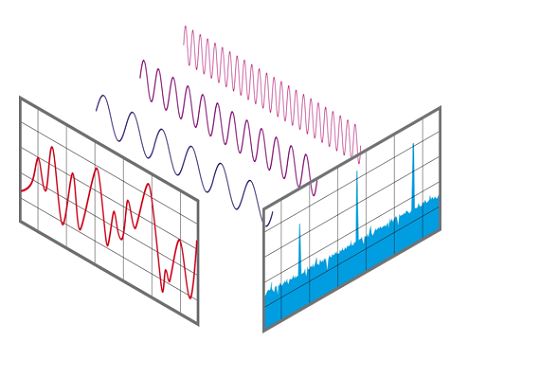
Another example
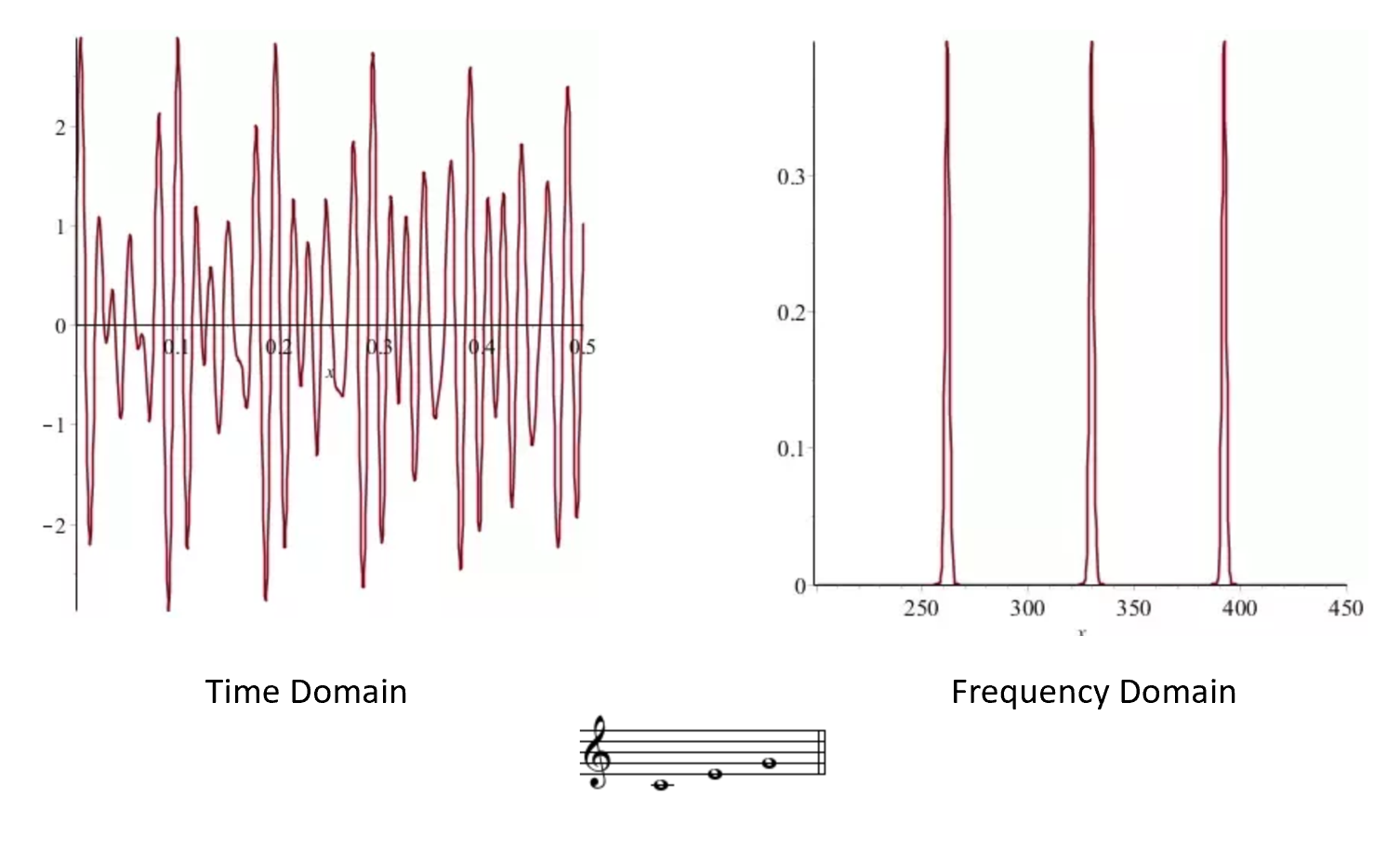
And another

And another
Fast Fourier transform

In 1965, Americans wanted to find way to detect Soviet nuclear experiments from seismic data. Can do so with Fourier transform
Problem: Lots of data, Fourier transform too slow
John Tukey came up with “Fast Fourier Transform”: improve running time from \(n^2\) to \(n \log n\): thousand or million times speedup!
Tukey couldn’t publish so collaborated with James Cooley for chemistry application.
On every “top 10 algorithms” list. Applications include signal processing, compression, spectroscopy, engineering, earth sciences, optics, crystallography, …
The story continues
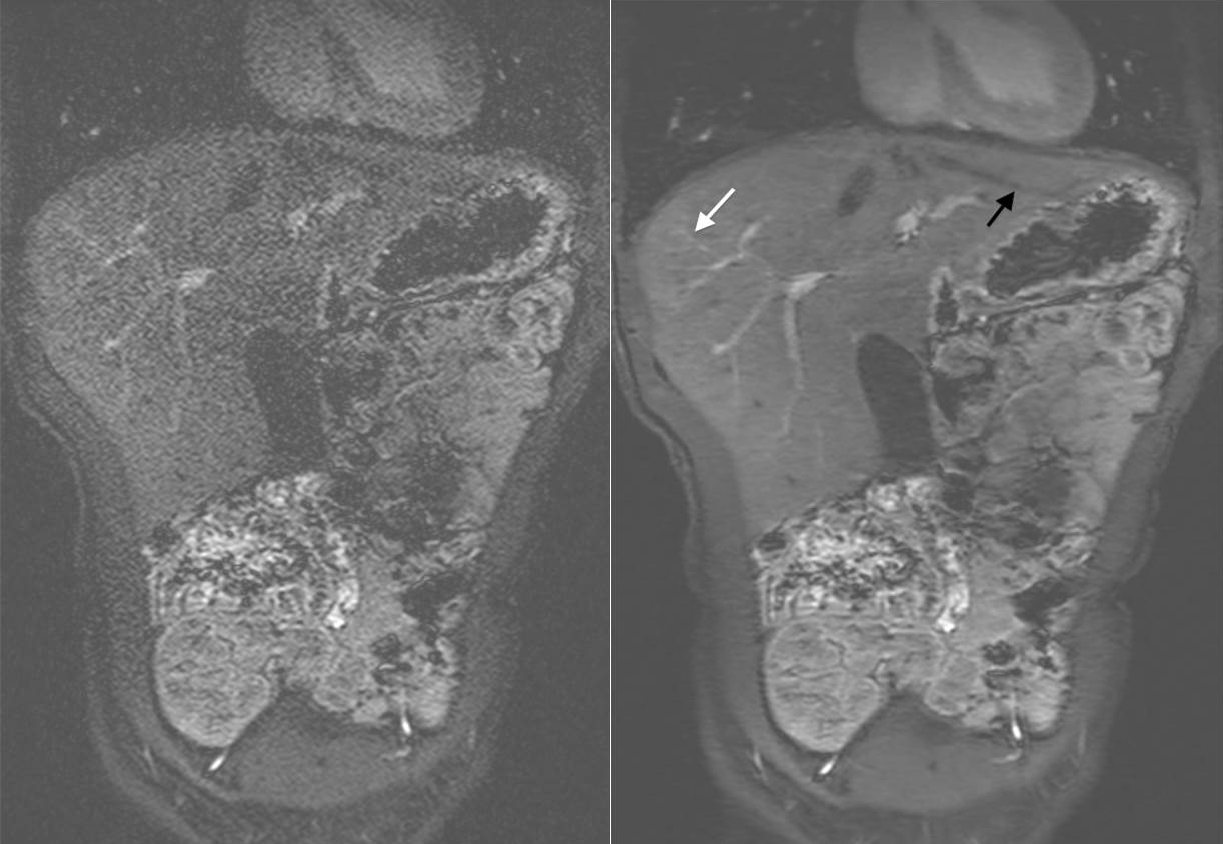
Compressed sensing
MRI Imaging:
- Run MRI to get \(N\) pixels \(f(0),\ldots,f(N-1)\)
- Do (sort of) Fourier Transform to \(F\) and find coefficients \(\alpha_0,\ldots,\alpha_{N-1}\).
- “Denoising/compression”: Remove frequencies with small coefficients, keep \(n \ll N\) coefficients.
Q: Can we “skip the middle man” and do MRI with only \(n\) observations?
A: Yes! “Compressed Sensing” (Candes-Romberg-Tao 2006). Sometimes life vs death difference!
Key insight
Given linear equations \(Ax= b\), can find “short” solution \(x \in \mathbb{R}^n\), minimizing \(\sum |x_i|\). “Linear Programming”
Can we do the same for integer \(x \in \mathbb{Z}^n\)? No! (this course)

Miklos Ajtai and Cynthia Dwork 1997: A public key cryptosystem based on difficulty of this problem.
Our current best hope for “post quantum cryptography”
Other algorithms
Google was founded on the PageRank algorithm for a approximating top eigenvector of a random walk matrix.
Backpropagation algorithm is driving much of deep learning, based on computing symbolic derivatives of arithmetic circuits.
Akamai was founded on the consistent hashing data structure for a distributed dynamic hash table.
Was any company founded based on the non existence of algorithm?
Yes! RSA, and many others…
CS 121
Why take this course?
because you have to..
Take this course to
Understand the greatest scientific revolution of 20th (and 21st) centuries.
The ideas that underlie the technologies we use.
New way of thinking
New lens on other phenomena
- Connections to compilers and programming languages and systems and machine learning and security and physics and pure math (and biology, statistics, economics, law, philosophy)
On difficulty
The fundamental equation of college
Hard + Required = Sucks
Why is CS 121 hard?
CS 121 is difficult: need to learn new concepts, acquire a new way of thinking
Other difficult tasks:
- Learning a second language
- Learning how to program
- Mastering a musical instrument
- Playing competitive sports
(Getting into Harvard..)
CS 121 Math
Typical introductory math: Student executes an algorithm.
(solve equations, compute derivatives and integrals, manipulate trigonometric functions, etc..)
In CS 121: Analyze algorithms (prove properties of algorithm \(A\)), even meta analyze algorithms (prove existence/non-existence of algorithm of type \(P\))
Good news: It’s a different kind of hard. More thinking, less remembering or calculating.
Bad news: It’s a different kind of hard.
The P word
Lots of proofs in this course.
proof: prüf , noun
A sequence of logical deductions that starts from some axioms and ultimately arrives at a conclusion.
proof: prüf , noun
A ritual in which a sequence of meaningless formulas is written under an obvious statement.
A proof is a piece of English text that convinces a knowledgeable but skeptical reader that a statement X is true beyond a shadow of a doubt.
To write a proof:
- Understand precisely what X means.
- Convince yourself that X is true.
- Sketch the argument on a pad/board/napkin to yourself or a friend.
- Write and rewrite until the reasoning is crystal clear and as simple as you can make it.
Don’t go to step \(i+1\) before completing step \(i\).
Err on the side of being more precise.
The D word
Even more important (and often harder!) than proofs are definitions.
If you don’t understand what X means, how can you prove it?
CS 121 reading
Before every lecture you’ll need to read 20-30 pages of mathematical text.
Bad news: It will be slow at start
Good news: One of the most transferable skills.
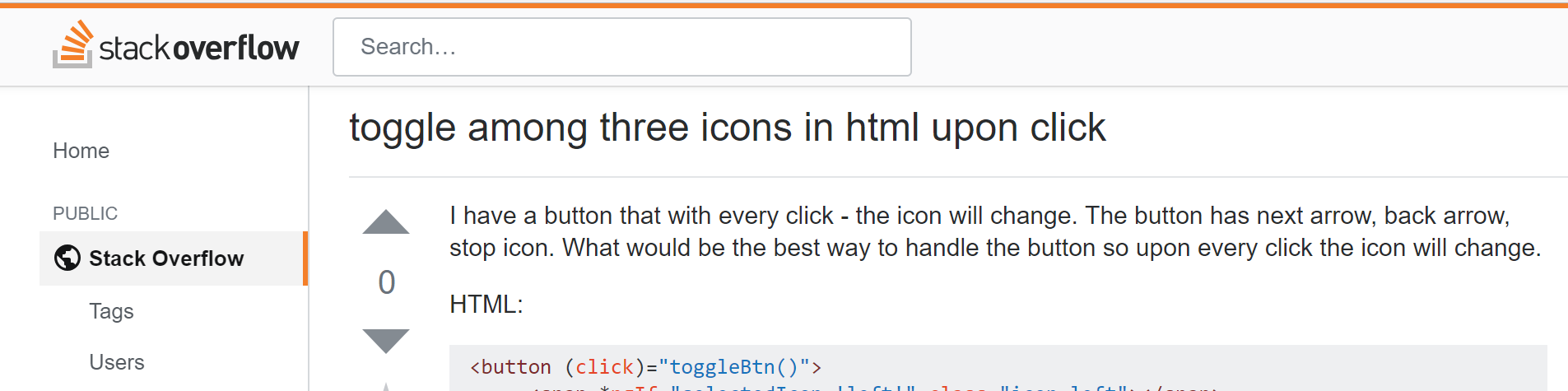
Would you rather read this?
Or this
Do I have a “math brain”?
No No one has: we execute math reasoning on our “run-from-lions” processor.
Variations in aptitude (mostly speed) and confidence (not very correlated to performance)
Most important trait for succeeding in math (and life) is grit.
Focus on your own growth
Is it all about innate talent?
Being tall helps in rock climbing.

Ashima Shiraishi, age 17, Height 5’ 1".
Is it worth it?
“It’s still hard to explain what can be so fascinating about beating your head against the wall for three days, not knowing how to solve something the better way, the beautiful way. But once you find that way, it’s the greatest feeling in the world.”
L. Torvalds, programmer.
This course is hard but…
We have your back
- Textbook
- Lectures
- Sections
- “Proof workshop”, special sections
- Piazza boards
- Office hours
- BSC Tutoring
- Patel Fellow: Eric Liu
We have your back
Surviving (and thriving in!) CS 121
- Read the text before each lecture
- Read the text before each lecture
- Ask questions! Here, in office hours, Piazza.
- Collaborate, but do the problem sets.
- Be curious but critical, ask why are we learning this.
- Read carefully the syllabus (16 min 27 sec according to read-o-meter)
- Several bonus, makeup opportunities. Don’t need to be perfect to get an A.
- Embrace the challenge and even the frustration.
- Use us, use and help your peers.
- Keep at it even when it’s hard, and even when it’s easy.
(Ask us about “advanced section / CS 121.5”)
Surviving (and thriving in!) this week
Put the course on your crimson cart so you are in canvas.
Join Piazza, download app, activate notifications- our main/only method of communication!
Do Homework zero (bonus) by Thursday night and submit via gradescope.
Read “Chapter 2: representation” today or tomorrow - do canvas quiz on it no later than Thursday 9:30am.
If you didn’t read Chapter 0 and Chapter 1 yet: do so asap.
Pizza Party on Friday 12pm!
Sneak preview
We will define a computational model:
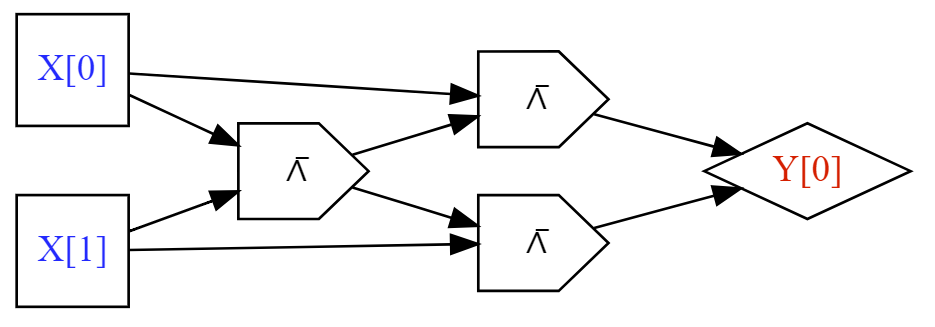

\(((2, 0, 1), (3, 0, 2), (4, 1, 2), (5, 3, 4))\)
Need to understand functions, sets, tuples, strings, graphs.
Sneak preview (2)
- Universality: program that can evaluate other programs
- Self replication: program that can print its own code
- Hardness: are some functions inherently uncomputable? intractable?
Sneak preview (3)
- Gödel’s incompleteness theorem
- λ calculus
- Regular expressions, context free grammar.
- Computational difficulty - P and NP
- Randomness in computation
- Cryptography, quantum computing
Pizza Party - Friday 12pm - Ground floor Maxwell-Dworkin
Join Piazza and Canvas
Fill survey at http://tiny.cc/121initialsurvey
CS 121 web page: cs121.boazbarak.org or Google “CS 121 Boaz”