Lecture 2
Lecture 2: Representing objects as strings
Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow), Yueqi Sheng (Advanced section), Chi Ning Chou (Advanced section).

Laptops/phones only on last 5 rows please.
Announcements
- Proof workshop!
- Pizza party tomorrow 12pm-2pm MD lobby
- Survey: tiny.cc/121initialsurvey
- HW1 out today, due Wednesday 11:59pm, see collaboration policy. Declare pairs on tiny.cc/121pairs
CS 121 components
- Textbook: Read deeply to learn the concepts
- Lectures: Second exposure: go over high level concepts, consolidate understanding.
- Sections: Work through examples and techniques in smaller groups.
- Problem sets: Solidify skills and knowledge through practice.
- Piazza: Ask questions as you go through reading and psets.
- Office hours: Individual help in working through concepts.
Tips:
- Make sure you are prepared for lecture
- Start early on psets and reading
- Expect some problems to be challenging.
- Know when and how to seek help.


“Digital representations have been catalyzed by computers, but they are fundamentally about the symbols, not the technology that records them, and they were with us long before any of our current electronic devices.”
“With the discovery that a cell’s protein content is encoded using three-letter words written in an alphabet of four genetic bases, the field of biology stumbled upon an ancient digital representation of remarkable sophistication and power.”
What is computation?
One definition: Mapping input to output.
“Axiom:” All our inputs and outputs can be encoded as binary strings of finite length.
“Algorithm \(A\) multiplies two numbers” is really
“Given the encoding of \(x\) and \(y\), \(A(x,y)\) outputs the encoding of \(x\times y\)”
Representation and Computation
Choosing representation makes a difference
- Compression: representation with small size (e.g., JPEG)
- Error correction: representation that is robust to errors (e.g., “control digits”, error correcting codes)
- Data structures: representation enabling fast operations (e.g., binary numbers, distance oracles)
- Feature extraction: representation enabling prediction (e.g., deep nets)
- Secrecy: representation hiding certain information (e.g., encryption, commitment)
Our focus: Some representation of objects as strings.
What is “the number \(17\)”?
What is “the number \(17\)”?
- \(17\)
- XVII
- \((1,0,0,0,1)\)
- 0x11
The “thing outside the cave” whose shadows are the above?
Doesn’t matter?
Definition of representation:
Set \(\mathscr{O}\) of objects
Examples:
- Numbers
- Text
- Images
- MRI scans
- Matrices
- Graphs
- Computer programs
- …
Definition of representation:
A representation of \(\mathscr{O}\) as \(\mathscr{R}\) (usually \(\mathscr{R}=\{0,1\}^*\)) consists of:
Encoding function \(E:\mathscr{O} \rightarrow \mathscr{R}\)
Decoding function \(D:\mathscr{R} \rightarrow \mathscr{O}\)
Example 1: Representing natural numbers via binary basis:
- \(D(x_0,\ldots,x_{n-1})=x_0 + x_1\cdot 2^1 +\cdots + x_{n-1}\cdot 2^{n-1}\).
- \(E(o) = (x_0,\ldots, x_{n-1})\) s.t. \(x_i = \lfloor \tfrac{x}{2^i} \rfloor \mod 2\) for \(i \in [n]\).
Example 2: Represent graphs as adjacency matrix
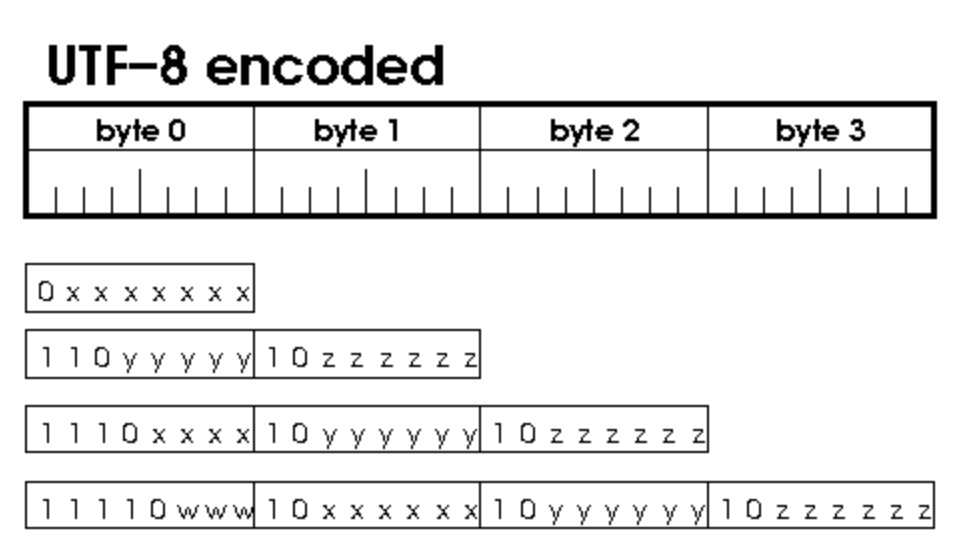
Example 3: Represent English text as ASCII or UTF-8 strings
Which of the following statements is not necessarily true: pollev.com/cs121
a The encoding function always has to be one to one
b The decoding function always has to be onto
c The functions satisfy \(D(E(o))=o\) for every \(o\in\mathscr{O}\).
d The functions satisfy \(E(D(y))=y\) for every \(s\in\mathscr{R}\).
Definition of representation:
A representation of \(\mathscr{O}\) as \(\mathscr{R}\) (usually \(\mathscr{R}=\{0,1\}^*\)) consists of:
- Encoding function \(E:\mathscr{O} \rightarrow \mathscr{R}\) which is 1-to-1.
Decoding function \(D:\mathscr{R} \rightarrow \mathscr{O}\) which is onto.
\(E,D\) satisfy \(\color{red}{(*)}\): \(D(E(o))=o\) for every \(o\in\mathscr{O}\).
Definition of representation:
A representation of \(\mathscr{O}\) as \(\mathscr{R}\) (usually \(\mathscr{R}=\{0,1\}^*\)) consists of:
1. Encoding function \(E:\mathscr{O} \rightarrow \mathscr{R}\) which is 1-to-1.
2. Decoding function \(D:\mathscr{R} \rightarrow \mathscr{O}\) which is onto.
3. \(E,D\) satisfy \(\color{red}{(*)}\): \(D(E(o))=o\) for every \(o\in\mathscr{O}\).
Theorem For every pair of sets \(\mathscr{O} , \mathscr{R}\), the following are equivalent:
There exists a representation \((E,D)\) of \(\mathscr{O}\) in \(\mathscr{R}\).
There exists a one-to-one \(E:\mathscr{O} \rightarrow \mathscr{R}\).
There exists an onto \(D:\mathscr{R} \rightarrow \mathscr{O}\).
\(|\mathscr{O}| \leq |\mathscr{R}|\)
Make sure you know how to prove this
Transitivity of representation
Claim: If \(E: \mathscr{O} \rightarrow \mathscr{R}\) and \(F: \mathscr{R} \rightarrow \mathscr{S}\) are 1-to-1, then their composition \(F \circ E\) is 1-to-1.
Corollary: If we can represent objects in \(\mathscr{O}\) as objects in \(\mathscr{R}\), and can represent objects in \(\mathscr{R}\) as strings in \(\{0,1\}^*\), then can represent \(\mathscr{O}\) as strings.
Example: \(\mathscr{O}\) = Python programs. \(\mathscr{R}\) = English text.
Corollary: Can represent Python programs as binary strings.
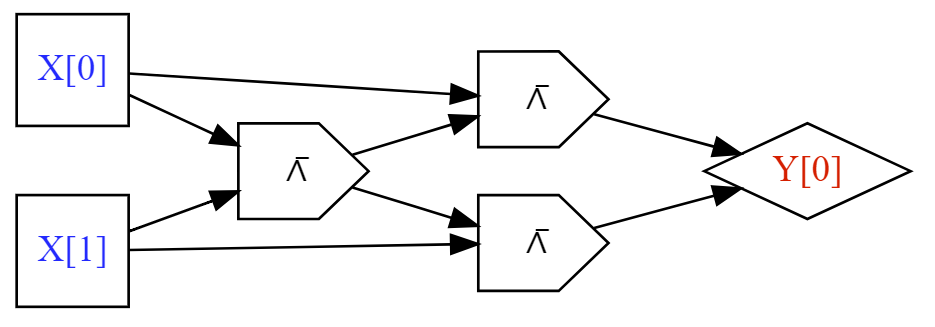
Prefix freeness
Def: Representation \(E:\mathscr{O} \rightarrow \{0,1\}^*\) is prefix free if there are no \(o\neq o'\) such that for every \(i \in [|E(o)|]\), \(E(o)_i = E(o')_i\).
English is not prefix free: teacher stalking.com
Prefix free encoding of English words: use spaces sentences (list of words) : use spaces and periods
Prefix freeness
Def: Representation \(E:\mathscr{O} \rightarrow \{0,1\}^*\) is prefix free if there are no \(o\neq o'\) such that for every \(i \in [|E(o)|]\), \(E(o)_i = E(o')_i\).
Examples:
- Binary representation of \(\mathbb{N}\) to \(\{0,1\}^*\).
- Binary representation of \([1000]\) to \(\{0,1\}^{10}\) with leading zeroes.
- UTF-8 representation of symbols.
Making every representation prefix free
- Modify \(E:\mathscr{O} \rightarrow \{0,1\}^*\) to prefix-free \(E:\mathscr{O} \rightarrow \{0,1,;\}^*\)
- Compose with representation \(E':\{0,1,;\} \rightarrow \{ 0,1 \}^2\)
Cost: \(n \mapsto 2n+2\).
Exercises:
Give encoding mapping \(n\) length strings to at most \(2\lceil \log n \rceil + 2 + n\) bits.
Give encoding mapping \(n\) length strings to at most \(2\log\log n + 100 + \lceil \log n \rceil + n\) bits.
Offline: Show no such encoding mapping \(n\) length strings to less than \(n + 0.99\log n + 1000\) bits. (Kraft’s Inequality)
Huffman codes: Prefix free encoding with minimum average length.
In future: Interchange \(F(x,y,z)\) with \(F(xyz)\).
Encoding strings
- “C Style” - null terminated string: Represent \(s_0,\ldots,s_{n-1} \in \{1,\ldots,255 \}\) as \((s_0,s_1,\ldots,s_{n-1},0)\)
Easy code to copy:
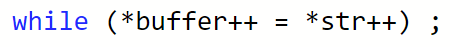
- “Pascal style” - length-prefix string: Represent \(s_0,\ldots,s_{n-1}\in \{0,\ldots,255 \}\) with \(n \leq 255\) as \((n,s_0,\ldots,s_{n-1})\) (variants with more bytes: \(4\) bytes suffices for \(2^{32}=1GB\) )
Quickly compute len(s)
Tradeoffs between memory use and efficiency of operations
Buffer overflows..
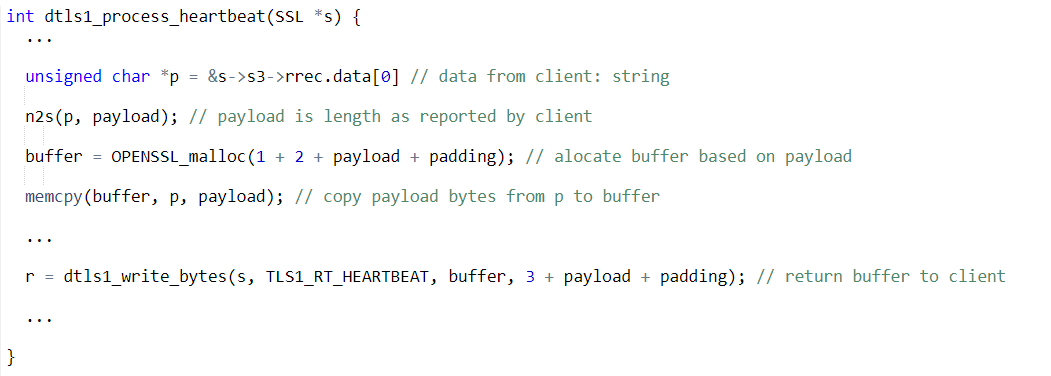
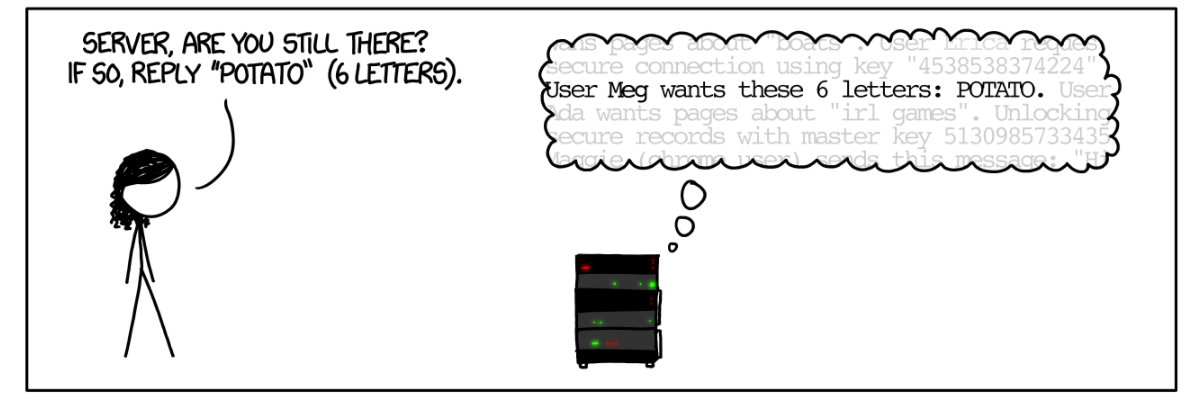
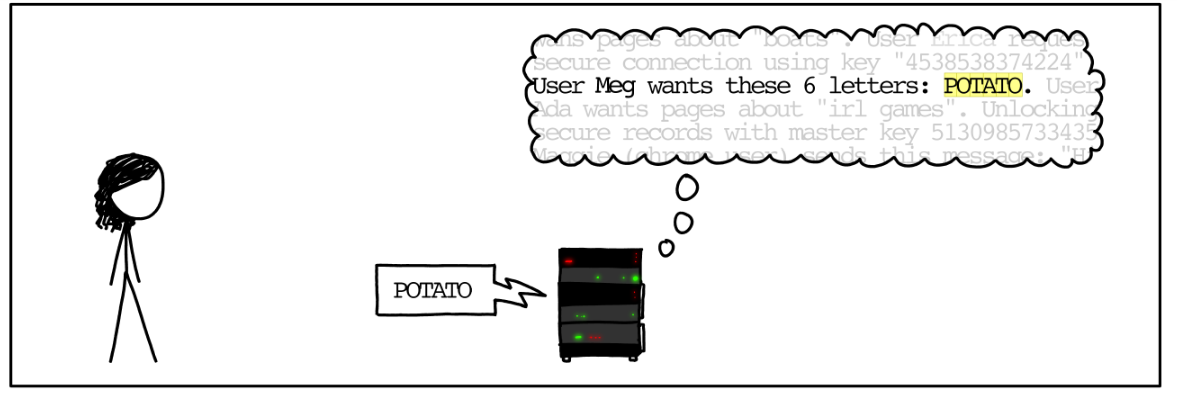
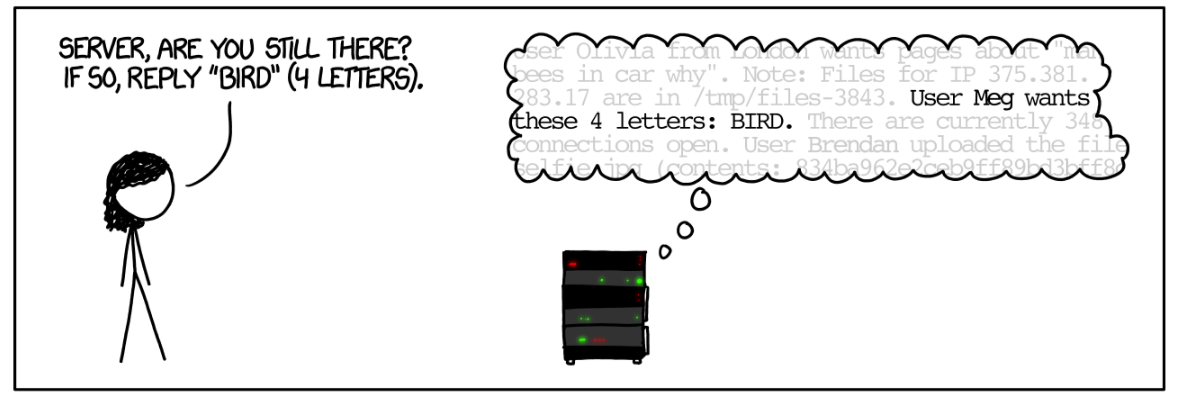
TLS Heartbeat protocol
Goal: Check connection with server, keep it alive
Client to Server: Send string \(s\)
Server to Client: Send \(s\) back
Concretely: \(s\) represented as \((payload,p)\), where \(payload \in \mathbb{N}\), \(p \in \{0,1\}^*\), \(payload = |p|\).
Heartbleed
Heartbleed
Heartbleed

Heartbleed
“Some might argue that it is the worst vulnerability found (at least in terms of its potential impact) since commercial traffic began to flow on the Internet.”, Joseph Steinberg , Forbes.
Representing anything?
“Axiom”: Can represent anything as zeroes and ones.
What about real numbers? Say between \(0\) and \(1\)?
Represent \(3/8 = 1/4 + 1/8\) as \(0.011\) in binary.
What about \(1/10\)? Or \(1/3\)? Represent \(a/b\) as \((a,b)\).
What about \(1/\pi\)?
Unfortunate fact
Thm: (Cantor, 1874) No 1-to-1 map \(RtS:\mathbb{R} \rightarrow \{0,1\}^*\)
aka Reals are uncountable
aka \(|\mathbb{R}| \gt |\mathbb{N}|\)
aka \(\aleph \gt \aleph_0\).
Unfortunate fact
Thm: (Cantor, 1874) No 1-to-1 map \(RtS:\mathbb{R} \rightarrow \{0,1\}^*\)
Lemma 1: Exists 1-to-1 map from \(FtR:\{0,1\}^\infty \rightarrow \mathbb{R}\)
(\(\{0,1\}^\infty = \{ f \;|\; f:\mathbb{N}\rightarrow \{0,1\} \}\))
Lemma 2: No onto map \(StF:\{0,1\}^* \rightarrow \{0,1\}^\infty\).
Lemma 1 + Lemma 2 implies thm:
Lemma 1: Exists 1-to-1 map from \(FtR:\{0,1\}^\infty \rightarrow \mathbb{R}\).
Proof: For every \(f \in \{0,1\}^\infty\) (i.e. \(f:\mathbb{N}\rightarrow \{0,1\}\)) define
One to one because \(f(i) \neq f'(i)\) implies \(|FtR(f)-FtR(f')| \gt \tfrac{8}{9} \cdot 10^{-i}\).
Lemma 2: No onto map \(StF:\{0,1\}^* \rightarrow \{0,1\}^\infty\).
Since there exists onto map \(\mathbb{N}\rightarrow \{0,1\}^*\), this is equivalent to:
Lemma 2’: No onto map \(NtF:\mathbb{N}\rightarrow \{0,1\}^\infty\).
First step of proof: Understand what is needed to prove: Inexistence of function \(NtF:\mathbb{N}\rightarrow \{0,1\}^\infty\) which is onto. Every \(NtF:\mathbb{N}\rightarrow \{0,1\}^\infty\) is not onto.
not onto: There exists \(f^* \in \{0,1\}^\infty\) such that for every \(n\in \mathbb{N}\), \(NtF(n) \neq f^*\).
\(\{0,1\}^\infty\) : Set of functions mapping \(\mathbb{N}\) to \(\{0,1\}\).
Equality of functions \(g,f^* \in \{0,1\}^\infty\): \(g = f^*\) iff for every \(m\in \mathbb{N}\), \(g(m)=f^*(m)\).
Inequality of functions \(g,f^* \in \{0,1\}^\infty\): \(g \neq f^*\) iff there exists \(m\in \mathbb{N}\) s.t. \(g(m) \neq f^*(m)\).
Need to show: For every \(NtF:\mathbb{N}\rightarrow \{0,1\}^\infty\), there exists \(f^* \in \{0,1\}^\infty\) s.t. for every \(n\in \mathbb{N}\), there exists \(m\in \mathbb{N}\) s.t. \(NtF(n)(m) \neq f^*(m)\).
Lemma 2’: No onto map \(NtF:\mathbb{N}\rightarrow \{0,1\}^\infty\).
Proof: Find \(f^* \in \{0,1\}^\infty\) s.t. \(f^* \neq NtF(n)\) for every \(n\)
That is, for every \(n\) there is \(m\) s.t. \(f^*(m) \neq NtF(n)(m)\).

Representing reals
Floating point: Given budgets \(k,\ell\), represent \(x\in \mathbb{R}\) as \((a,b) \in \mathbb{Z}^2\) with \(|a| \leq 2^k\), \(|b|\leq 2^\ell\) such that \(|x- a2^{b}|\) is minimal.
Cost: \(\sim\) \(2+k+\ell\) bits.
Accuracy: Can represent numbers in \([-2^k,+2^k]\) up to \(2^{k-\ell}\) error.
IEEE 754 double precision floating point (Javascript “number”, Python “float”, C “double”*: \(64\) bits: \(\sim\) \(k=53\), \(\ell=11\).
single precision: \(32\) bits: \(\sim\) \(k=24\), \(\ell=8\).
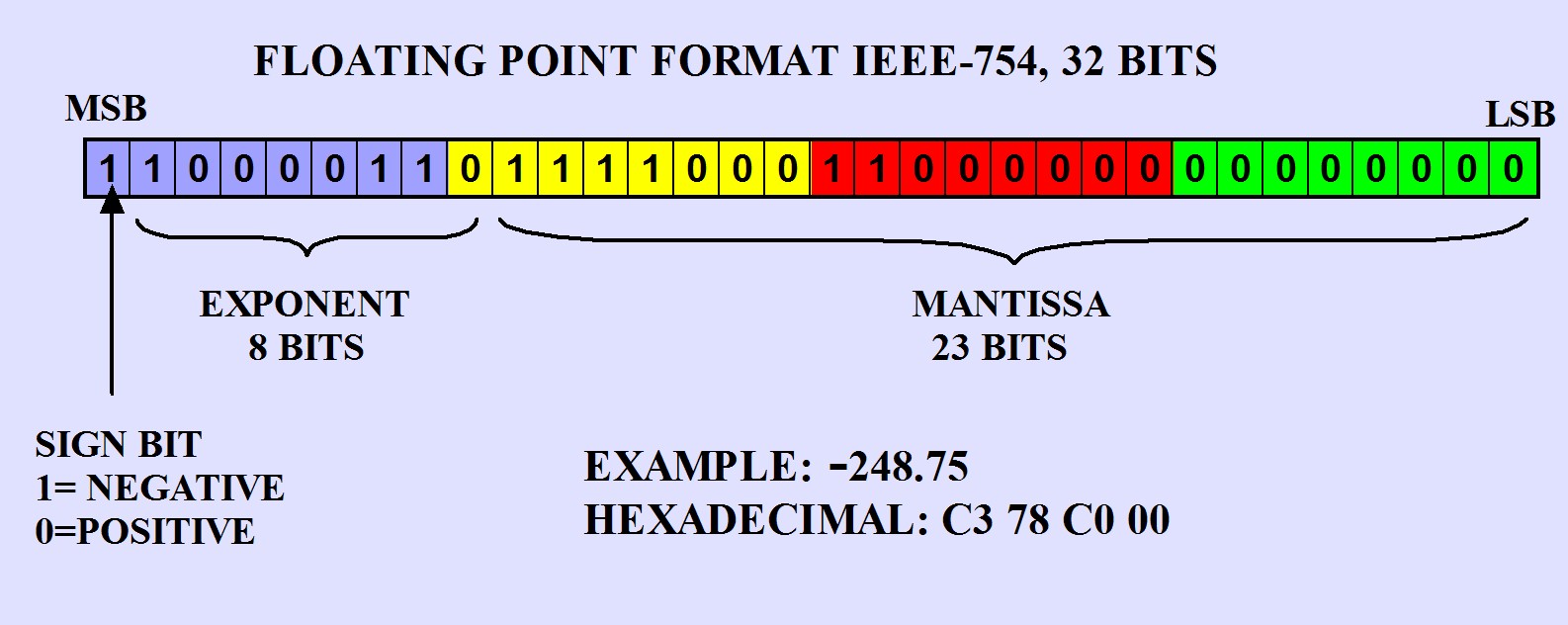
Floating point issues
Rule of thumb: Avoid floats if you can. Money and time are not floats.
Patriot anti-missile system: Time kept in units of \(1/10\)-th of second. Stored as 24 bit binary fraction + 24 bit whole number. Inaccuracy of roughly \(2^{-24} \approx 10^{-7}\). Accumulates to about \(0.35\) seconds after \(100\) hours, since this is \(100 \times 3600 \times 10 = 3.6 \times 10^6\) 10th of seconds.

Using \(48\) bit integers we could store number of 10th of seconds for a million years with no overflow.
Arianne 5


Some thoughts on math
Proofs and programs
- Understand the question
- Get high level idea how to solve it
- Work out outline on napkin / pad / whiteboard
- Write down plugging all gaps
“Debugging” proofs:
- Type safety: If proofs refers to \(x\), what is it? where did it come from? what do we know about it? why can we assume it exists?
- Scope: For every sentence/equation, what argument does it belong to? Is it part of a proof of an intermediate claim? is this a fact established from the previous arguments? Is this a new claim that will need to be proved?
Cargo Cult Proofs

Cargo Cult Science, Richard Feynmann, 1974
Cargo Cult Proofs
A proof is not about the ritual, symbols, rules, conventions.

A proof is an air-tight argument that the statement is true.
Conventions are designed to help ensure this.
Coming up: Defining computation