CS 121, Lecture 8 NAND++

N or Space for next slide, P for previous slide, F for full screen, M for menu

Lec 6: NAND++

Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow)

Laptops/phones only on last 5 rows please.

Sipser

Infinite functions

Up till now: Talked about finite functions \(F:\{0,1\}^n \rightarrow \{0,1\}^m\)

Today: First introduction to infinite functions \(F:\{0,1\}^* \rightarrow \{0,1\}^*\)

Or is it?

\(PROD:\mathbb{N}\times \mathbb{N}\rightarrow \mathbb{N}\). Equivalently \(PROD:\{0,1\}^* \rightarrow \{0,1\}^*\)

NAND++

Which of the following functions is computable by a NAND++ program? pollev.com/cs121

a. \(ADD(a,b) = a + b\).

b. \(MULTIPLY(a,b) = a \cdot b\)

c. \(LOG(a,b) = \max \{c \in \mathbb{N}: b^c \leq a \}\).

d. All of the above

NAND++

Which of the following functions is computable by a NAND++ program? pollev.com/cs121

a. \(ADD(a,b) = a + b\).

b. \(MULTIPLY(a,b) = a \cdot b\)

c. \(LOG(a,b) = \max \{c \in \mathbb{N}: b^c \leq a \}\).

d. All of the above

Why NAND++?

Goal: Compute infinite function \(F:\{0,1\}^* \rightarrow \{0,1\}\) with finite set of instructions.

Need to handle \(\text{Input length} \gg \text{Program length}\).

Repeat same instructions many times. Loops!

Allow access to memory \(\gg\) program length. Arrays!

NAND + LOOPS + Indexing = NAND++

NAND++ features

Go back to beginning at the end as long as loop. Effectively


do {
 ...code...
} until loop==False

Arrays via the special index variable i. Variable such as Temp[i] replaced with Temp[\(val\)] where \(val\) is current value of i

Index variable i in enhanced NAND++ controlled via i += foo , i -= foo operations.

In vanilla NAND++ travels obliviously in sequence \(0,1,0,1,2,1,0,1,2,3,2,1,0,1,\ldots\). “T vs Uber” f . . .

\[Index(\ell) = \min_r |\ell - r(r+1)|\]

NAND++ view 2

If \(P\) is a vanilla NAND++ program, to execute \(P\) on \(x\in \{0,1\}^*\) do:

Let \(n=|x|\). Initialize the variables X[0] … X[\(n-1\)] to \(x_0,\ldots,x_{n-1}\). Initialize Xvalid[0] … Xvalid[\(n-1\)] to \(1\).

Set \(\ell=0\), \(t=0\).

Do “search and replace” on the code of \(P\) replacing i with \(\ell\).

Run the lines of \(P\) as it was a NAND program, updating all variables accordingly.

If loop \(= 0\) then break and output Y[0]…Y[\(m-1\)] where \(m\) is the smallest such that Yvalid[\(m\)] \(=0\).

Otherwise set \(t= t+1\), \(\ell = Index(t)\) and go back to 3.

Exercise: Break out in groups and explain the above to one another. Make sure you understand why this is equivalent to the definition in the book.

NAND++ view 2

If \(P\) is a vanilla NAND++ program, to execute \(P\) on \(x\in \{0,1\}^*\) do:

Let \(n=|x|\). Initialize the variables X[0] … X[\(n-1\)] to \(x_0,\ldots,x_{n-1}\). Initialize Xvalid[0] … Xvalid[\(n-1\)] to \(1\).
Set \(\ell=0\), \(t=0\).
Do “search and replace” on the code of \(P\) replacing i with \(\ell\).
Run the lines of \(P\) as it was a NAND program, updating all variables accordingly.
If loop = 0 then break and output Y[0]…Y[\(m-1\)] where \(m\) is the smallest such that Yvalid[\(m\)] \(=0\).
Otherwise set \(t= t+1\), \(\ell = Index(t)\) and go back to 3.

Exercise: “unrolling the loop”

Exercise: Suppose that \(P\) is a NAND++ program that computes a function \(F:\{0,1\}^* \rightarrow \{0,1\}\). Suppose that moreover that for every \(x\in \{0,1\}^n\), the number of lines that \(P\) executes before it halts is always at most \(n^2\).

Prove that there is a NAND program \(Q\) with \(n\) inputs and one output and at most \(10\cdot n^2\) lines, such that for every \(x\in \{0,1\}^n\), \(Q(x)=F(x)\).

Exercise: “unrolling the loop”

Prove that there is a NAND program \(Q\) with \(n\) inputs and one output and at most \(10\cdot n^2\) lines, such that for every \(x\in \{0,1\}^n\), \(Q(x)=F(x)\).

Turing machine

Models person with:

Unbounded sheet of paper (“tape”)
Finite working memory (“states”)
Each step: Read/Write one symbol, update memory, move to adjacent tape location.

Example: Person computing \(a \times b\) using gradeschool algorithm.

Question: Why did Turing try to model a person and not an electronic computer?

Turing machine simulator

https://turingmachinesimulator.com

Exercise: what is constant

Talk in groups and decide which of the following quantities is constants - have bounded size independent of how long the input is:

The number of lines in a NAND++ program
The number of states in a Turing machine
The maximum value that the index variable i achieves in a NAND++ execution.
The rightmost position that the head of a Turing machine reaches during an execution.
The number of symbols in the alphabet of a Turing machine.
The number of variable identifiers in a NAND++ program.
The number of bits needed to describe a Turing machine’s state transition function.

Exercise: what is constant

Talk in groups and decide which of the following quantities is constants - have bounded size independent of how long the input is:

The number of lines in a NAND++ program
The number of states in a Turing machine
The maximum value that the index variable i achieves in a NAND++ execution.
The rightmost position that the head of a Turing machine reaches during an execution.
The number of symbols in the alphabet of a Turing machine.
The number of variable identifiers in a NAND++ program.
The number of bits needed to describe a Turing machine’s state transition function.

What is a constant?

The NAND++ program size, NAND++ number of variables, Turing machine states, alphabet and state transition are fixed in advance. (before we get the input)

The number of execution steps of NAND++/TM, position of index variable /head all depend on the input length. (grow with the input length)

The point of NAND++/Turing machines: A constant sized recipe how to execute an unbounded in advance number of operations.

High level takeaway

What is computation? Local evolution of global state according to a finite set of instructions.

DNA, physical systems, bee colonies, slime mould, markets..

Syntactic sugar: \(i+= foo\) and \(i-= bar\)

Three types of memory access:

Oblivious: Topology is fixed in advance independent of input. (NAND, vanilla NAND++, Hardware, Internet,..)

Sequential: Memory is one dimensional array, can travel on it one step at a time. (enhanced NAND++ with \(i++/i--\) sugar, Turing machines)

Random access: Memory is array/dictionary, can access memory at any address at unit cost. (RAM machines, programming languages)

Vanilla to enhanced NAND++

Question: How do we implement i+= foo and i -= bar in NAND++?

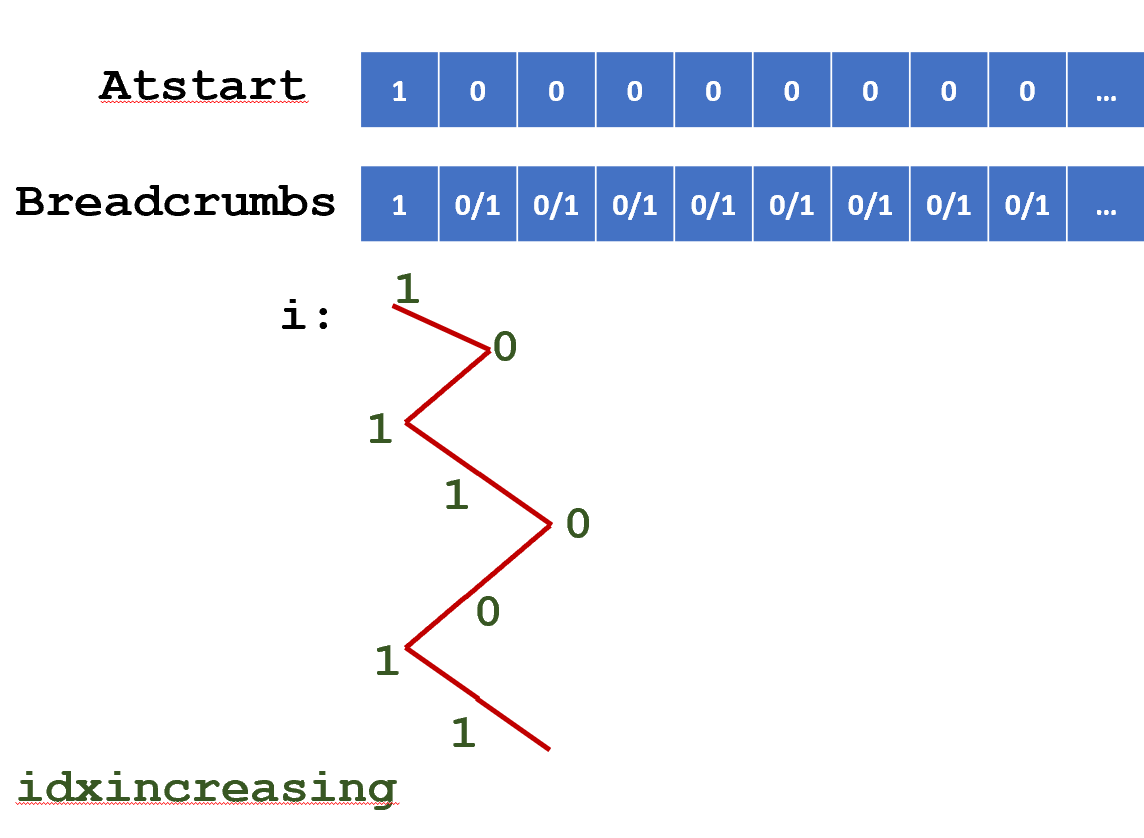
Answer: “Breadcrumbs” and “wait for bus strategy”

Atstart array initialized to \((1,0,0,0,\ldots)\)

Breadcrumbs array initialized to \((0,0,\ldots)\), Breadcrumbs[i] set to \(1\) at the end of every loop

indexincreasing set to \(1\) when at Atstart[i]\(=1\),set to \(0\) when observe a new place (Breadcrumbs[i]\(=0\)).

“Breadcrumbs” and “Wait for Bus”

Atstart array initialized to \((1,0,0,0,\ldots)\)
Breadcrumbs array initialized to \((0,0,\ldots)\), Breadcrumbs[i] set to \(1\) at the end of every loop
indexincreasing set to \(1\) when at Atstart[i]\(=1\),set to \(0\) when observe a new place (Breadcrumbs[i]\(=0\)).

Two-tape TMs = One-tape TMs

Exercise: Prove that \(F\) is computable by one-tape TM if and only if it is computable by two-tape TM.

Two-tape TMs = One-tape TMs

Exercise: Prove that \(F\) is computable by one-tape TM if and only if it is computable by two-tape TM.

Two-tape TMs = One-tape TMs

Idea: Odd location tape 1, Even location tape 2.

Add “marker” for heads location: \(\Sigma \mapsto \Sigma \times \{ m,u \}\)

Simulate one step:

Start in even location: go in jumps of two to find “even head” and read value.

Move to odd, find “odd head” and read value

Compute new state, vals to be written, directions.

Scan to find heads and update.

New state: \([k] \mapsto [k] \times [k'] \approx [k\times k']\)

Types of results in CS 121

Computation results: Function \(F\) is computable in model \(A\). Mathematically: Show exists program/machine \(P\) in model \(A\) such that for every \(x\in \{0,1\}^*\), on input \(x\) program \(P\) outputs \(F(x)\).

Simulation/equivalence results: Every function \(F\) computable by model \(A\) is also computable by model \(B\). Mathematically: Show that for every program \(P\) in model \(A\), exists program/machine \(Q\) in model \(B\) such that for every \(x\in \{0,1\}^*\) on which \(P(x)\) outputs \(y\), \(Q(x)\) outputs \(y\) as well.

Interplay:

Use computation results to show equivalence results.
Once we have equivalence results, can prove computation results in the most convenient model.

Infinite loops


temp = NAND(X[0],X[0])
loop = NAND(X[0],temp)

For NAND programs: for every input \(x \in \{0,1\}^n\), \(P(x)\) produces an output \(y\in \{0,1\}^m\).

For NAND++ programs: some programs on some inputs might fail to halt.

NAND vs NAND++

NAND: No loops: \(s\) lines = \(s\) computational steps. Can access at most \(3s\) memory location. straightline program / circuit

NAND++: Loops: same line can be repeated in many steps: num steps \(\gg\) num lines Arrays: index variable moves between iterations: memory usage \(\gg\) num lines

Let \(XOR:\{0,1\}^*\) be such that \(XOR(x) = x_0 + x_1 + \cdots + x_{n-1} \mod 2\).

Theorem: There is NAND++ program \(P\) to compute \(XOR\).

It’s not that NAND can’t compute \(XOR\). It’s a category error!

Theorem: For every \(n\in \mathbb{N}\), there is a NAND program \(P_n\) to compute \(XOR_n\): restriction of \(XOR\) to inputs of length \(n\).

Next up

More proficient in understanding our models and moving between them.

Food for thought: Consider the function \(reverse:\{0,1\}^* \rightarrow \{0,1\}^*\) such that \(reverse(x_0 \cdots x_{n-1}) = x_{n-1}x_{n-2}\cdots x_0\).

Write a program to compute \(reverse\) in your favorite programming language

Think of you would write a NAND++ program to compute \(reverse\).

Same for Turing machine, \(\lambda\)-expression, NAND<< programs.

Configurations

At given point in time, can encode all of the memory contents and state of NAND++ program / Turing machine as finite string.

Length of string = O(number of steps so far)

Configuration at step \(\ell\) very similar to configuration at step \(\ell + 1\). Differs only in constant number of bits

Think in groups: How would you encode the configuration of a program as a string? You can be wasteful in space, but try to make sure that computing the next configuration from the previous one is as simple as possible. Choose vanilla/enhanced NAND++ or Turing machines as per your convenience