\renewcommand{}{}
N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 11: Efficient computation
Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow)

Laptops/phones only on last 5 rows please.
Today’s take aways
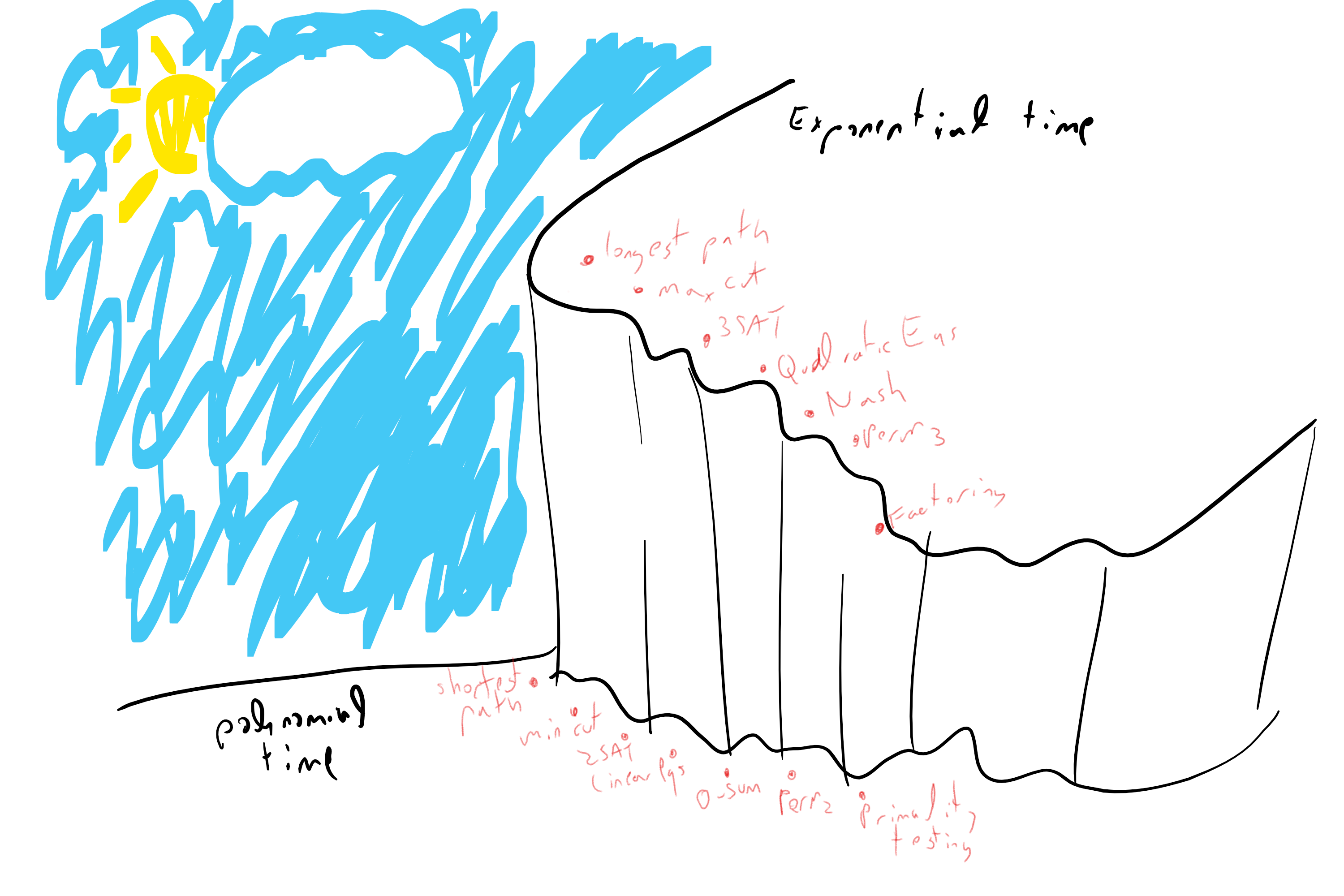
- Many problems have trivial/naive/“brute force”/“exhaustive search” exponential time algorithm (\(2^{poly(n)}\) or \(exp(n)\))
- Some have much faster polynomial time (\(poly(n)\), often even \(O(n)\) or \(O(n^2)\)) algorithms.
- Poly vs exponential difference sometimes more important than computable vs not
Today’s lecture
Measuring running time
Algorithmic techniques
Examples
Measuring running time
int mystery(int m) {
int i,j,k,s;
s = 0;
for(i=0;i < m; i++) {
for (j=0; j < m ; j++) {
for (k=0; k < m ; k++) {
if (k > j) { s = s+ 1; }
if (k < j) { s= s-1; }
}
}
}
return s;
}What is the running time of mystery as a function of \(m\)? a) \(O(\log m)\) b) \(O(m)\) c) \(O(m^3)\) d) \(2^{O(m)}\)
Measuring running time
int mystery(int m) {
int i,j,k,s;
s = 0;
for(i=0;i < m; i++) {
for (j=0; j < m ; j++) {
for (k=0; k < m ; k++) {
if (k > j) { s = s+ 1; }
if (k < j) { s= s-1; }
}
}
}
return s;
}What is the running time of mystery as a function of \(m\)? a) \(O(\log m)\) b) \(O(m)\) c) \(O(m^3)\) d) \(2^{O(m)}\)
Measuring running time
int mystery(int m) {
int i,j,k,s;
s = 0;
for(i=0;i < m; i++) {
for (j=0; j < m ; j++) {
for (k=0; k < m ; k++) {
if (k > j) { s = s+ 1; }
if (k < j) { s= s-1; }
}
}
}
return s;
}\(TIME(m) = O(m^3)\)
What is the running time of mystery as a function of \(n\) (input length)? a) \(O(\log n)\) b) \(O(n)\) c) \(O(n^3)\) d) \(2^{O(n)}\)
Measuring running time
int mystery(int m) {
int i,j,k,s;
s = 0;
for(i=0;i < m; i++) {
for (j=0; j < m ; j++) {
for (k=0; k < m ; k++) {
if (k > j) { s = s+ 1; }
if (k < j) { s= s-1; }
}
}
}
return s;
}\(TIME(m) = O(m^3)\)
What is the running time of mystery as a function of \(n\) (input length)? a) \(O(\log n)\) b) \(O(n)\) c) \(O(n^3)\) d) \(2^{O(n)}\)
Measuring running time II
int mystery2(int m) {
if (m < 1) { return 1; }
return mystery2(m-1)+mystery2(m-1);
}What function does mystery compute?
Measuring running time II
int mystery2(int m) {
if (m < 1) { return 1; }
return mystery2(m-1)+mystery2(m-1);
}What function does mystery compute?
Measuring running time II
int mystery2(int m) {
if (m < 1) { return 1; }
return mystery2(m-1)+mystery2(m-1);
}What is its running time as a function of \(m\)? a \(O(\log m)\) b \(O(m)\) c \(O(m^2)\) d \(2^{O(m)}\)
Measuring running time II
int mystery2(int m) {
if (m < 1) { return 1; }
return mystery2(m-1)+mystery2(m-1);
}What is its running time as a function of \(m\)? a \(O(\log m)\) b \(O(m)\) c \(O(m^2)\) d \(2^{O(m)}\)
\(T(m) = 2\cdot T(m-1) + O(1)\).
When happens if we replace last line with
return 2*mystery2(m-1);?
Data structures
Lists: Store ordered tuple \((a_0,\ldots,a_{n-1})\). (Can implement stacks, queues)
Dictionaries: Store \((key,value)\) pairs, retreive by key. (arrays: special case where keys are in \([n]\))
Search trees: Dictionaries with “range queries”
Graphs: Store edges, queries such as predecessor, successor, distance.
In all cases Easy implementations with \(poly(n)\) time, \(poly(n)\) storage \(n\)= number of elements / bits
Clever implementations reduce \(O(n^2)\) to \(O(n)\), \(O(n)\) to \(O(\log n)\) etc.
Back to math
Linear equations
Input: \(n\) linear equations in \(n\) variables: \(Ax=b\), with \(A\in \mathbf{R}^{n \times n}\) and \(b \in R^n\).
Output: “No solution” or assignment satisfying equations.
Notation: Equations are \(\langle A^i,x \rangle=b_i\) where \(A_i\) is \(i\)-th row of \(A\), and \(\langle u,v \rangle=\sum_{j=0}^{n-1} u_iv_i\).
Linear equations
Input: \(n\) linear equations in \(n\) variables: \(Ax=b\), with \(A\in \mathbf{R}^{n \times n}\) and \(b \in R^n\).
Output: “No solution” or assignment satisfying equations.
Gaussian elimination Algorithm:
- If \(n=1\): trivial
- Rearrange equations, variables, so that \(A^0_0 \neq 0\). (first equation involves first variable)
- Change equation from \(\langle A^0,x \rangle=b_0\) to \(\tfrac{1}{A^0_0}\langle A^0,x \rangle=\tfrac{b_0}{A^0_0}\). i.e., \(\color{red}{x_0 = b_0 - \sum_{j=1}^{n-1} v_j x_j \;\; (*)}\) where \(v_j=\tfrac{A^0_j}{A^0_0}\).
- Replace \(x_0\) with RHS of \(\color{red}{(*)}\) in equations \(1,\ldots,n-1\).
- Now have \(n-1\) equations with \(n-1\) variables!
Analysis: \(T(n)= \text{number of arithmetic operations}\) then \(T(n)=O(n^2)+T(n-1)\). Solves for \(T(n)=O(n^3)\) Actual time includes polynomial factor in bit length. All amounts to polynomial time
Calculus
If \(f:\mathbf{R}\rightarrow \mathbf{R}\) is “nice” then a local minimum of \(f\) is \(x\) with \(f'(x)=0\) and \(f''(x)\gt0\).
If \(f''(x)\gt0\) everywhere then \(f\) is convex and local minimum = global minimum.
Can find local minimum by gradient descent: Change \(x\) to \(x - \eta f'(x)\).
Multivariate calculus

- \(f:\mathbf{R}^n \rightarrow \mathbf{R}\) is convex if \(f(px+(1-p)y) \leq pf(x)+ (1-p)f(y)\).
- \(f\) is convex \(\Rightarrow\) global minimum = local minimum
- generalizes to \(f:K \rightarrow \mathbf{R}\) where \(K\) is convex set
- can use gradient descent to optimize
- For “nice” functions \(f\) and sets \(K\) have algorithms with polynomial time worst-case performance.
Linear programming
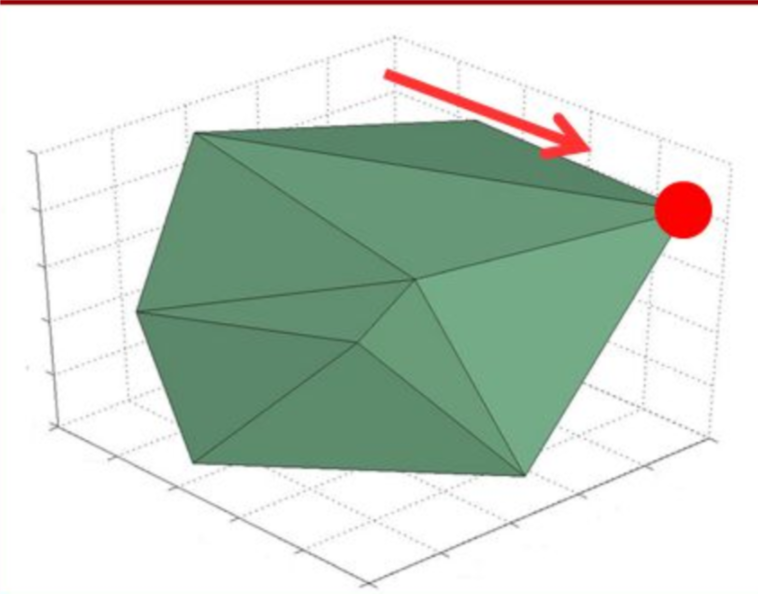
Compute \(\min_{x\in K} f(x)\) where \(f\) is linear and \(K\) is polytope:
\(K = \{ x\in \mathbf{R}^n \;|\; Ax \leq b \}\)
Linear programming
Compute \(\min_{x\in K} f(x)\) where \(f\) linear and \(K = \{ x\in \mathbf{R}^n \;|\; Ax \leq b \}\)
Example: Startup resource allocation:
Supporting a business customer costs \(a\) developer hours and \(b\) customer support hours, and gives \(r\) revenue.
Supporting an end user costs \(a'\) dev hours, \(b'\) support hours, and gives \(r'\) revenue.
Maximize revenue subject to \(A\) total dev hours and \(B\) total support hours:
Why can we do max and not min?
Thm: (Khachiyan 79, Karmakar 84) There is \(poly(n)\) time algorithm for linear programming on \(n\) variables.
Integer programming
Compute \(\min_{x\in I} f(x)\) where \(f\) linear and \(I = \{ x\in \mathbb{Z}^n \;|\; Ax \leq b \}\). i.e., integer solutions only
Motivation: Can’t support half a client
Depressing fact: No known polynomial time algorithm for integer programming.
Better news: Highly tuned exponential time algorithms can handle from hundreds to thousands of variables. But integrality still barrier to clean theory, understanding.
Minimum \(s,t\) cut problem
Def: A cut in \(G=(V,E)\) is \(S \subseteq V\) with \(\emptyset \neq S \neq V\).
Edges cut by \(S\) are \(E(S,\overline{S})\)
Minimum \(s,t\) cut problem
Def: A cut in \(G=(V,E)\) is \(S \subseteq V\) with \(\emptyset \neq S \neq V\).
Min \(s,t\) cut: Minimize \(|E(S,\overline{S})|\) over all \(S\subseteq V\) s.t. \(s\in S\) and \(t\not\in S\) (sample motivation: image segmentation)
Minimum \(s,t\) cut problem
Def: A cut in \(G=(V,E)\) is \(S \subseteq V\) with \(\emptyset \neq S \neq V\).
Min \(s,t\) cut: Minimize \(|E(S,\overline{S})|\) over all \(S\subseteq V\) s.t. \(s\in S\) and \(t\not\in S\)
Max \(s,t\) flow: Maximize flow from \(s\) to \(t\). (sample motivation: routing)
Minimum \(s,t\) cut problem
Def: A cut in \(G=(V,E)\) is \(S \subseteq V\) with \(\emptyset \neq S \neq V\).
Min \(s,t\) cut: Minimize \(|E(S,\overline{S})|\) over all \(S\subseteq V\) s.t. \(s\in S\) and \(t\not\in S\)
Max \(s,t\) flow: Maximize flow from \(s\) to \(t\).
Max Flow Min Cut Thm: Maximum \(s,t\) flow \(=\) minimum \(s,t\) cut
\(\leq\): If cut has value \(k\) then can’t move more than \(k\) units from left to right.
\(\geq\): If every cut is not “tight”, can “improve” flow
Corollary: Can solve min \(s,t\) cut in polynomial time. (and also global minimum cut)
Maximum cut problem
Find cut \(S\) that maximizes \(|E(S,\overline{S})|\). Sample applications: Ising model, also related to X-ray crystallography, cryo-electron microscopy, more
Depressing news: Best known algorithms are exponential in the worst case.
Better news: Algorithms that give approximately maximal cut are known.
Even better news: Techniques from above algorithms used elsewhere: Phase retrieval for crystallography, Robust principal component analysis for dynamic MR, super resolution for background extraction and imaging
Maximum cut as integer program
Maximum cut:
Input: \(G=(V,E)\) of \(m\) edges
Goal: Find cut \(\emptyset \neq S \neq V\) maximizing \(|E(S,\overline{S})|\).
IP: Find \(x \in \mathbb{Z}^n\) and \(y\in \mathbb{Z}^m\) maximizing \(\sum_{j=0}^{m-1} y_j\) s.t.
- \(0 \leq x_i \leq 1\) and \(0 \leq y_j \leq 1\) for \(i \in [n]\) and \(j\in [m]\) (i.e., \(x\in \{0,1\}^n\) and \(y\in \{0,1\}^m\))
- If \(j\)-th edge is \((u,v)\) then \(y_j \leq x_u + x_v\) and \(y_j \leq 2 - x_u - x_v\).
Corollary: Poly time algorithm for INTEGER PROGRAMMING implies poly-time algorithm for MAX CUT.
\(3\)-SAT problem
Input: A formula on \(n\) variables of the form \(C_0 \wedge C_1 \wedge \cdots \wedge C_{m-1}\) where \(C_i\) is OR of three variables or their negations.
Example: \((x_7 \vee \overline{x}_17 \vee x_{29}) \wedge (\overline{x}_7 \vee x_{15} \vee x_{22} ) \wedge (x_{22} \vee \overline{x}_29 \vee x_{55})\)
Goal: Find out if there is assignment \(x\in \{0,1\}^n\) that makes formula true.
Depressing news: Best known algorithms require exponential time.
Better news: Exponent has improved, decent heuristic “SAT SOLVERS”, can solve the 2SAT problem.
Problem: Suppose you could solve INTEGER PROGRAMMING in poly time. Show that you can solve 3SAT in poly time.
\(3\)-SAT problem
Input: A formula on \(n\) variables of the form \(C_0 \wedge C_1 \wedge \cdots \wedge C_{m-1}\) where \(C_i\) is OR of three variables or their negations.
Example: \((x_7 \vee \overline{x}_17 \vee x_{29}) \wedge (\overline{x}_7 \vee x_{15} \vee x_{22} ) \wedge (x_{22} \vee \overline{x}_29 \vee x_{55})\)
Goal: Find out if there is assignment \(x\in \{0,1\}^n\) that makes formula true.
Problem: Suppose you could solve INTEGER PROGRAMMING in poly time. Show that you can solve 3SAT in poly time.
\(3\)-SAT problem as IP
Input: A formula on \(n\) variables of the form \(C_0 \wedge C_1 \wedge \cdots \wedge C_{m-1}\) where \(C_i\) is OR of three variables or their negations.
Goal: Find out if there is assignment \(x\in \{0,1\}^n\) that makes formula true.
Maximize over \(x\in \mathbb{Z}^n\) and \(y \in \mathbb{Z}^m\) the value \(\sum_{j=0}^{m-1} y_j\) s.t.
- \(x\in \{0,1\}^n\) and \(y\in \{0,1\}^m\). (i.e., \(0 \leq x,y \leq 1\))
- If clause \(j\) is \((\overline{x}_{17} + x_{55} + x_{22})\) then add constraint \((1-x_{17}) + x_{55} + x_{22} \geq y_j\).
Surprising fact: If you can solve 3SAT in poly time then you can solve INTEGER PROGRAMMING in poly time!
\(k\)-coloring problem
Input: Graph \(G=(V,E)\), number \(k\)
Goal: Find if can color vertices using \(k\) colors so that no two neighbors have same color. (Sample motivation: GSM frequency assignment)
\(k\)-coloring problem
Input: Graph \(G=(V,E)\), number \(k\)
Goal: Find if can color vertices using \(k\) colors so that no two neighbors have same color.
4 Color Theorem: For every planar graph, can do so (in poly time!) for \(k=4\). Conjectured by Guthrie in 1852, proven by Appel-Haken 1976 via induction with about 2,000 base cases.
Depressing fact: We don’t know better than exponential algorithm for \(k \geq 3\) for general graphs. No better than exponential algorithm for \(k = 3\) for planar graphs.
Better news: We do have poly time algorithm for \(k=2\).
Problem: Show that if you can solve INTEGER PROGRAMMING then you can solve 3-coloring
\(k\)-coloring problem
Input: Graph \(G=(V,E)\), number \(k\)
Goal: Find if can color vertices using \(k\) colors so that no two neighbors have same color.
Problem: Show that if you can solve INTEGER PROGRAMMING then you can solve 3-coloring