CS 121, Lecture 12 Modeling Efficient computation

\renewcommand{}{}

N or Space for next slide, P for previous slide, F for full screen, M for menu

Lec 12: Modeling Efficient computation

Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow)

Laptops/phones only on last 5 rows please.

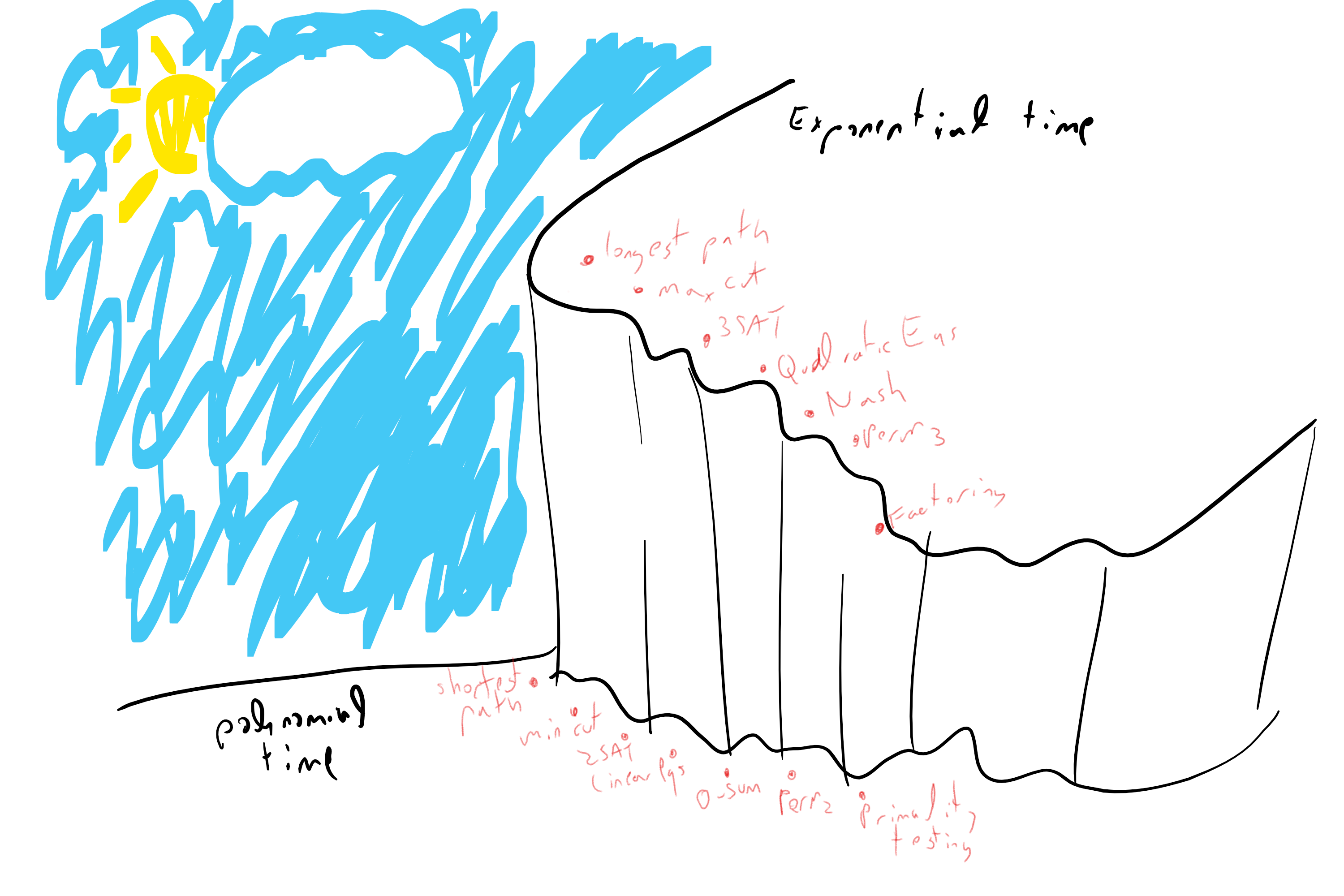
Prezi

Modeling Running Time

Lesson No 1: Running time is function, not a number

Examples: \(T(n)=100n\), \(T(n)=10\cdot n^2\), \(T(n)=2^n\), etc. etc.

Def: \(F: \{0,1\}^* \rightarrow \{0,1\}\) is in \(TIME(T(n))\) if there exists \(P\) s.t. for every large enough \(n\) and every \(x\in \{0,1\}^n\) , \(P\) halts within \(T(|x|)\) steps with output \(F(x)\).

Question 1: If we change exists to for every what would be the effect on set \(TIME(1000n)\)?

a) It would stay the same
b) It would become empty
c) It would contain \(HALT\)
d) None of the above

Modeling Running Time

Lesson No 1: Running time is function, not a number

Def: \(F: \{0,1\}^* \rightarrow \{0,1\}\) is in \(TIME(T(n))\) if there exists \(P\) s.t. for every large enough \(n\) and every \(x\in \{0,1\}^n\) , \(P\) halts within \(T(|x|)\) steps with output \(F(x)\).

Question 1: If we change exists to for every what would be the effect on set \(TIME(1000n)\)?

a) It would stay the same
b) It would become empty
c) It would contain \(HALT\)
d) None of the above

Modeling Running Time

Lesson No 1: Running time is function, not a number

Def: \(F: \{0,1\}^* \rightarrow \{0,1\}\) is in \(TIME(T(n))\) if there exists \(P\) s.t. for every large enough \(n\) and every \(x\in \{0,1\}^n\) , \(P\) halts within \(T(|x|)\) steps with output \(F(x)\).

Question 2: If we change every to there exists what would be the effect on set \(TIME(1000n)\)?

a) It would stay the same
b) It would become empty
c) It would contain \(HALT\)
d) None of the above

Modeling Running Time

Lesson No 1: Running time is function, not a number

Def: \(F: \{0,1\}^* \rightarrow \{0,1\}\) is in \(TIME(T(n))\) if there exists \(P\) s.t. for every large enough \(n\) and every \(x\in \{0,1\}^n\) , \(P\) halts within \(T(|x|)\) steps with output \(F(x)\).

Question 2: If we change every to there exists what would be the effect on set \(TIME(1000n)\)?

a) It would stay the same
b) It would become empty
c) It would contain \(HALT\)
d) None of the above

Choosing the model

Lesson 2: At coarse enough resolution, model doesn’t matter.

Def of computable invariant under model: NAND++, NAND<< , RAM machines, Turing Machines, Cellular automata, \(\lambda\) calculus, Game of life, etc..

Def of \(TIME(T(n))\) is not invariant under model: exists \(F \in TIME_{\lt\lt}(100n)\) but \(F\not\in TIME_{++}(n^{1.1})\).

Q: Is there \(F \in TIME_{++}(100 n) \setminus TIME_{\lt\lt}(n^{1.1})\)? a) yes, b) no

Choosing the model

Lesson 2: At coarse enough resolution, model doesn’t matter.

Def of computable invariant under model: NAND++, NAND<< , RAM machines, Turing Machines, Cellular automata, \(\lambda\) calculus, Game of life, etc..

Def of \(TIME(T(n))\) is not invariant under model: exists \(F \in TIME_{\lt\lt}(100n)\) but \(F\not\in TIME_{++}(n^{1.1})\).

Q: Is there \(F \in TIME_{++}(100 n) \setminus TIME_{\lt\lt}(n^{1.1})\)? a) yes, b) no

Choosing the model

Lesson 2: At coarse enough resolution, model doesn’t matter.

Def of computable invariant under model: NAND++, NAND<< , RAM machines, Turing Machines, Cellular automata, \(\lambda\) calculus, Game of life, etc..

Def of \(TIME(T(n))\) is not invariant under model: exists \(F \in TIME_{\lt\lt}(100n)\) but \(F\not\in TIME_{++}(n^{1.1})\).

Definition of \(\mathbf{P}\) and \(\mathbf{EXP}\) are invariant under model: NAND++, NAND<<, RAM machines, Turing machines, \(\lambda\) calculus*, etc… (Extended Church-Turing Thesis)

This course: mostly don’t care about difference of \(n^2\) vs \(n^5\).

In practice and other areas of theory: Care deeply. Use RAM models and more refined models and measures of resources: space, paralelism, communication, cache locality, …

Interlude: Nice functions

Def: \(T:\mathbb{N}\rightarrow \mathbb{N}\) is nice if \(T(n) \geq n\), \(T(n) \leq T(n+1)\) (more time for longer inputs) and \(T\) is itself in time \(T\) (program knows when to stop).

Q: Why include \(T(n) \geq n\) in requirements?

We only care about nice functions: \(n,n^2,1000n^3\log n,3^n\), etc..

\(NAND_{\lt\lt}\) vs \(NAND_{++}\)

Trivial: \(TIME_{++}(T(n)) \subseteq TIME_{\lt\lt}(T(n))\) for every \(T\).

Thm: There are constants \(a,b\) (less than \(10\)) s.t. \(TIME_{\lt\lt}(T(n)) \subseteq TIME_{++}(a T(n)^b)\)

Proof: Go back to proof that computability is same for both models, and count number of steps.

NAND<< to NAND++ reduction 1

Features: integer variables | arithmetic operations | arithmetic with index

Step 1: Simulate integer arrays with two dimensional bit arrays

Cost: \(O(bit size) = O(\log T)\) overhead: \(O(T)\) length integer array mapped to \(O(T \log T)\) length bit array

Step 2: Simulate two dimensional arrays with one dimensional arrays

Cost: Total memory stays the same \(O(T\log T)\) bits, \(polylog(T)\) overhead to compute index.

Step 3: Implement arithmetic operations on bit-representations of integers.

Cost: School algorithms: \(O(poly(\log T))\) overhead

NAND<< to NAND++ reduction 2

Step 4: Use \(i++\) and \(i--\) to move index to location in integer array foo

Approach: Shift marker and decrement foo until it is zero.

Cost: \(O(T^2)\)

Step 5: Implement \(i++\) and \(i--\) in NAND++?

Approach: “Breadcrumbs” and “wait for bus strategy”

Cost: Number of steps grows from \(T'\) to \(O(T'^2)\).

Total cost: \(O(T^4 poly(log T))\)

Bottom line

Up to poly overhead:

\[NAND++ \;\approx\; NAND\lt\lt \;\approx\; TM \;\approx\; RAM \;\approx\; \lambda\]

Extended Church Turing Thesis: True for all physically realizable models.

Universal Machine:

Evaluating NAND<< programs:

Maintain dictionary Var_numbers mapping variable names to numbers in \(0\ldots t-1\): Var_numbers[name]=value

Maintain values of variables in array Var_values. For array variable Foo with Var_numbers[Foo]=s, store Foo[i] in Var_values[i*t+s]

Repeat execution until Var_values[Var_numbers[“loop”]]==0

Running time to simulate for \(T\) steps is \(O(T)\) steps.

Cor: Universal Interview Answer

Q: Write an \(O(n\log n)\) program to do task “blah”

A: Enumerate over all programs and test each one

from itertools import product
import string

def BLAH(x):
    n = 1
    while True:
        # iterate over all length n programs
        symbols = string.ascii_letters+string.digits+" \n+-*/=(){},''"
        for program in product(symbols, repeat=n):
            y = eval(''.join(program),x) # eval prog on x
            if TESTBLAH(x,y): return y
        n += 1

If there exists \(C\) character program solving BLAH in \(T(n)\) time, and running time to test Blah is \(Q(n)\), then running time is \(O(2^C \cdot (T(n)+Q(n)))\).

Time hierarchy theorem

Thm: For every nice \(T:\mathbb{N}\rightarrow \mathbb{N}\), \(TIME(T(n) \log n) \nsubseteq TIME(T(n))\)

note: Can replace \(\log n\) with any nice function \(f(n)\) going to infinity.

Pf: Bounded Halting function \(HALT_T\) designed so that:

(i) \(HALT_T \not\in TIME(T(n))\)

(ii) \(HALT_T \in TIME(T(n)\log n)\)

\(HALT_T(P,x) = 1\) iff \(|P| \leq \log\log |x|\) and \(P(x)=1\) within \(T(n)\sqrt{\log n}\) steps. \(n=|P|+|x|\)

(ii) follows immediately from \(TIMEDEVAL \in TIME(O(|P|T))\)

Proving time hierarchy thm

\(HALT_T(P,x) = 1\) iff \(|P| \leq \log\log |x|\) and \(P(x)=1\) within \(T(n)\sqrt{\log n}\) steps.

Lemma: \(HALT_T \not\in TIME(T(n))\)

Pf: Suppose \(H\) solves \(HALT_T\) in \(T(n)\) steps.

Program \(D(x)\):
1. If \(x\) not of form \(P10^k\) then loop
2. If \(H(P,P10^k)=1\) then loop

Let \(k\) large enough so \(|D| \leq \log\log k\) and \(n=2|D|+1+k\).

If \(H(D,D10^k)=1\) then \(D(D10^k)\) loops. But then \(H(D,D10^k)=0\)!

If \(H(D,D10^k)=0\) then \(D(D10^k)\) halts within \(O(n)+T(n) = O(T(n))\) steps. But since \(T(n)\sqrt{\log n} = \omega(T(n))\), this means that \(H(D,D10^k)=1\)!

Asymptotic Analysis

Abstract away implementation detail.

Focus on scaling behavior:
- \(O(n)\) time: doubling the input size doubles the time. \(c(2n)=2cn\)
- \(O(n^2)\) time: doubling the input size quadruples the time. \(c(2n)^2=4cn\)
- \(2^n\) time: adding one to the input doubles the time. \(2^{n+1}=2 \cdot 2^n\) doubling the input squares the time \(2^{2n}=(2^n)^2\)

Asymptotics and practice

Constants matter, especially in exponents

Refined measures matter (space, communication, caches)

Moore’s law doesn’t help: inputs grow with cycles as technlogy improvements

\(O(n)\) and \(O(n \log n)\) time algorithms executed in practice on petabyte size inputs (\(10^{15}\) bytes).

A \(2^n\) algorithm is beyond even nation-states for \(16\) bytes input (breaking AES-128).

Definitions

\(TIME(O(n)) = \cup_c TIME(c n)\)

\(\mathbf{P} = TIME(poly(n)) = \cup_{c} TIME(n^c)\)

\(\mathbf{EXP} = TIME(2^{poly(n)}) = \cup_c TIME(2^{n^c})\)

\(\mathbf{P}\), \(\mathbf{EXP}\) invariant under NAND++, NAND<< , TMs, RAM machines, ..

NAND vs NAND<< vs NAND++

Thm: If \(F \in TIME(T(n))\) then for every large enough \(n\), \(F_n \in SIZE(10 T(n))\). \(F_n\) is \(F\) restricted to \(\{0,1\}^n\)

Proof by Python:

def NANDppTONAND(P,n,T):
    res = ""
    for t in range(T):
        i = index(t) # value of i in T-th iteration
        valid = ('one' if i < n else 'zero' )
        res += P.replace('Xvalid[i]',valid).replace('[i]',f'[{i}]')
    return res

code not 100% correct

Exercise

Thm: If \(F \in TIME(T(n))\) then for every large enough \(n\), \(F_n \in SIZE(10 T(n))\). \(F_n\) is \(F\) restricted to \(\{0,1\}^n\)

Exercise 1: Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) has the property that \(F_n \not\in SIZE(n^{\log n})\) for every \(n\in \mathbb{N}\). Prove that \(F \not\in \mathbf{P}\).

Exercise

Thm: If \(F \in TIME(T(n))\) then for every large enough \(n\), \(F_n \in SIZE(10 T(n))\). \(F_n\) is \(F\) restricted to \(\{0,1\}^n\)

Exercise 1: Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) has the property that \(F_n \not\in SIZE(n^{\log n})\) for every \(n\in \mathbb{N}\). Prove that \(F \not\in \mathbf{P}\).

Exercise

Thm: If \(F \in TIME(T(n))\) then for every large enough \(n\), \(F_n \in SIZE(10 T(n))\). \(F_n\) is \(F\) restricted to \(\{0,1\}^n\)

Exercise 1: Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) has the property that \(F_n \not\in SIZE(n^{\log n})\) for every \(n\in \mathbb{N}\). Prove that \(F \not\in \mathbf{P}\).

Exercise 2: Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) has the property that \(F_n \in SIZE(n^2)\) for every \(n\in \mathbb{N}\). Which of the following is the case?

a \(F\) is necessarily in \(\mathbf{P}\).

b \(F\) is necessarily not in \(\mathbf{P}\).

c \(F\) can be sometimes in \(\mathbf{P}\) and sometimes outside \(\mathbf{P}\).

Exercise

Thm: If \(F \in TIME(T(n))\) then for every large enough \(n\), \(F_n \in SIZE(10 T(n))\). \(F_n\) is \(F\) restricted to \(\{0,1\}^n\)

Exercise 1: Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) has the property that \(F_n \not\in SIZE(n^{\log n})\) for every \(n\in \mathbb{N}\). Prove that \(F \not\in \mathbf{P}\).

Exercise 2: Suppose that \(F:\{0,1\}^* \rightarrow \{0,1\}\) has the property that \(F_n \in SIZE(n^2)\) for every \(n\in \mathbb{N}\). Which of the following is the case?

a \(F\) is necessarily in \(\mathbf{P}\).

b \(F\) is necessarily not in \(\mathbf{P}\).

c \(F\) can be sometimes in \(\mathbf{P}\) and sometimes outside \(\mathbf{P}\).

Relations to remember

\(TIME_{\lt\lt}(T(n)) \subseteq TIME_{++}(T(n)^c) \subseteq TIME_{\lt\lt}(T(n)^c)\). Corollary: “\(\mathbf{P_{++}} = \mathbf{P_{\lt\lt}} = \mathbf{P_{TM}}\)”

\(TIME(O(n)) \subsetneq \mathbf{P} \subsetneq \mathbf{EXP}\)

\(TIME(T(n)) \subsetneq SIZE(T(n)^5)\), \(\mathbf{P} \subsetneq \mathbf{P_{/poly}}\)

\(\mathbf{P_{/poly}}\) contains uncomputable functions:

If \(F\) is not in \(\mathbf{P_{/poly}}\) then it’s definitely hard.

If \(F\) is in \(\mathbf{P_{/poly}}\) then it might be easy.