\renewcommand{}{}
N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 18: Probability 101
Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow)

Laptops/phones only on last 5 rows please.
What is probability?
- Bayesians: Probability of \(A\) is your belief that \(A\) will occur. e.g., \(\mathbb{P}[\text{"rain tomorrow"}]=0.3\).
- Frequentists: Probability of \(A\) is the fraction of times (i.e., frequency) \(A\) occurs if we were to repeat experiment. e.g., \(\mathbb{P}[\text{"intervention better than control"}] \lt 0.05\)
- Mathematics: Probability of \(A \subseteq \Omega\) is \(\tfrac{|A|}{|\Omega|}\). (More generally: \(\mathbb{P}[A]=\sum_{a\in A}\mu(a)\) where \(\mu:\Omega\rightarrow [0,1]\), \(\sum_{x\in \Omega}\mu(x)=1\), or \(\mathbb{P}[A]=\int_{\Omega} 1_A d\mu\).)
For us: \(\Omega = \{0,1\}^n\): tossing \(n\) coins. \(\mathbb{P}[A]=|A|/2^n\).
What you need to know
What is the sample space (usually \(\{0,1\}^m\))
Events, union bound.
Random variables and expectation.
Conditioning and independence, Bayes’ rule
Concentration: Markov and Chernoff
Amplification
Less important for us: Continuous random variables, probability density functions, specific families such as Binomial, Geometric, Exponential, Negative Binomial, Hypergeometric, Poisson, Uniform, Normal, Gamma, Beta, chi-squared, student-t.
Question
What is \(\mathbb{P}_{x \sim \{0,1\}^n}[ \text{$4$ divides $n(x)$}]\) (\(n(x)\): number \(x\) represents in binary)
a. \(1/2\)
b. \(1/4\)
c. \(1/8\)
d. \(1/3\)
Union bound
Thm: If \(\mathbb{P}[A] \leq 0.1\) and \(\mathbb{P}[B] \leq 0.1\) then \(\mathbb{P}[A \cup B] \leq 0.2\)
Random variables
Def: Random variable is \(X:\{0,1\}^n \rightarrow \mathbf{R}\)
Expectation: \(\mathbb{E}[X] = 2^{-n}\sum_{x\in \{0,1\}^n} X(x)\)
Problem: Prove that if \(X(x) \leq Y(x)\) for every \(x\) then \(\mathbb{E}[X] \leq \mathbb{E}[Y]\).
Random variables
Def: Random variable is \(X:\{0,1\}^n \rightarrow \mathbf{R}\)
Expectation: \(\mathbb{E}[X] = 2^{-n}\sum_{x\in \{0,1\}^n} X(x)\)
Problem: Prove that if \(X(x) \leq Y(x)\) for every \(x\) then \(\mathbb{E}[X] \leq \mathbb{E}[Y]\).
Random variables
Def: Random variable is \(X:\{0,1\}^n \rightarrow \mathbf{R}\)
Expectation: \(\mathbb{E}[X] = 2^{-n}\sum_{x\in \{0,1\}^n} X(x)\)
Problem: Prove that if \(X(x) \leq Y(x)\) for every \(x\) then \(\mathbb{E}[X] \leq \mathbb{E}[Y]\).
Proof:
“Typical / likely” value of random variables
Expectation / mean: \(\mathbb{E}[X] = 2^{-n}\sum_{x\in \{0,1\}^n} X(x)\)
Median: Smallest \(\alpha\in \mathbf{R}\) such that \(\mathbb{P}[ X \geq \alpha ] \gt \geq 1/2\)
Mode(s): \(\alpha \in \mathbf{R}\) maximizing \(\mathbb{P}[ X = \alpha]\)
95% Confidence interval: minimum interval \(\alpha,\beta\) such that \(\mathbb{P}[ \alpha \leq X \leq \beta ] \geq 0.95\)
If \(X\) is “nice” then these are all similar. Proven using tail bounds
Often: With good probability \(X\) is within \(\mathbb{E}[X] \pm \sigma[X]\), where \(\sigma[X] = \sqrt{Var[X]}\). (\(Var[X] = \mathbb{E}[(X-\mu)^2]\) for \(\mu = \mathbb{E}[X]\).)
Markov’s Inequality
Thm: If \(X \geq 0\) and \(\mu = \mathbb{E}[X]\) then \(\mathbb{P}[X \geq k\mu ] \leq 1/k\)
Problem: Prove special case: If \(X \geq 0\) and \(\mathbb{E}[X]=1\) then \(\mathbb{P}[X \geq 100 ] \leq 0.1\)
Markov’s Inequality
Thm: If \(X \geq 0\) and \(\mu = \mathbb{E}[X]\) then \(\mathbb{P}[X \geq k\mu ] \leq 1/k\)
Problem: Prove special case: If \(X \geq 0\) and \(\mathbb{E}[X]=1\) then \(\mathbb{P}[X \geq 100 ] \leq 0.1\)
Drunkard’s walk
Line with locations \(\ldots,-3,-2,-1,0,+1,+2,+3,\ldots\)
Person starts at position \(0\), and each step goes right or left with probability \(1/2\) independently.
Drunkard’s walk
Person starts at position \(0\), and each step changes by \(+1\) or \(-1\) with probability \(1/2\) independently.
Interesting fact: After \(m\) steps will likely be in position that is roughly \(\pm \sqrt{m}\).
Intuition: Define \(X_i = \begin{cases} +1 & \text{step $i$ is left} \\ -1 & \text{otherwise} \end{cases}\)
Position at time \(m\) is r.v. \(X = \sum_{i=0}^{m-1} X_i\).
- \(\mathbb{E}[X] = \mathbb{E}[\sum_i X_i] = \sum_i \mathbb{E}[X_i] = 0\)
- \(Var[X]= \mathbb{E}[X^2]\) \(= \mathbb{E}[\sum_{i,j}X_iX_j]\) \(= \sum_{i,j}\mathbb{E}[X_iX_j]\) \(= \sum_{i=j}\mathbb{E}[X_i^2] + \sum_{i \neq j} \mathbb{E}[X_i]\mathbb{E}[X_j]\) \(=m \cdot \tfrac{1}{2} + 0\)
Hence if \(X\) is “nice” then it would “typically” be in the range \(0 \pm O(\sqrt{m})\).
Drunkard’s walk
Thm 1: After \(m\) steps, \(\mathbb{P}[ |\text{position}| \lt 1000 \sqrt{m}] \geq 0.99\)
Thm 2: After \(m\) steps, \(\mathbb{P}[ |\text{position}| \gt 0.001 \sqrt{m}] \geq 0.99\)
Proof of Theorem 1: Since \(\mathbb{E}[X^2] = m/2\), \(\mathbb{P}[ X^2 \gt 10^6m] \lt 0.001\) by Markov.
Proof of Theorem 2: Version with \(0.1\) instead of \(0.99\) follows from Paley Zygmund inequality: for \(Y\geq 0\), \(0 \leq \epsilon \leq 1\), \(\mathbb{P}[ Y \geq \epsilon \mathbb{E}Y ] \geq (1-\epsilon)^2\tfrac{\mathbb{E}[Y]^2}{\mathbb{E}[Y^2]}\).
Use that for \(Y = X^2\), \(\epsilon = 1/100\), together with \((*) \mathbb{E}[Y^2]=\mathbb{E}[X^4]=3n^2\).
(Prove \((*)\) using similar calculation as before)
2SAT Algorithm
Input: 2SAT formula \(\varphi\) with \(m\) constraints on \(n\) variables.
Operation:
Choose \(x \sim \{0,1\}^n\)
Repeat for \(100 n^2\) times:
If all clauses satisfied then return \(x\).
Pick random unsatisfied \((\neg)x_i \vee (\neg) x_j\) and flip at random either \(x_i\) or \(x_j\)
Analysis: Suppose \(\varphi\) has satisfying assignment \(x^*\). Let \(Z_i\) be number of variables on which \(x\) and \(x^*\) agree at step \(i\) of computation. If don’t halt \(Z_{i+1}= Z_i \pm 1\).
If clause \((\neg)x_i \vee (\neg) x_j\) is unsatisfied then \(x\) disagrees with \(x^*\) in at least one of \(x_i,x_j\). \(\Rightarrow \mathbb{P}[Z_{i+1}=Z_i+1] \geq 1/2\)
Worst case: \(Z_{i+1}=Z_i - 1\) w.p. \(1/2\), \(Z_{i+1}=Z_i+1\) w.p. 1/2 drunkard’s walk!
With constant probability will reach distance \(n\) from beginning after \(100n^2\) steps.
Correlation and concentration
Correlation and concentration

\(\mathbb{P}[ \text{Trump wins PA ∧ FL ∧ OH ∧ MI}] \sim 0.4^4 \sim 0.0256\)

Correlation and concentration
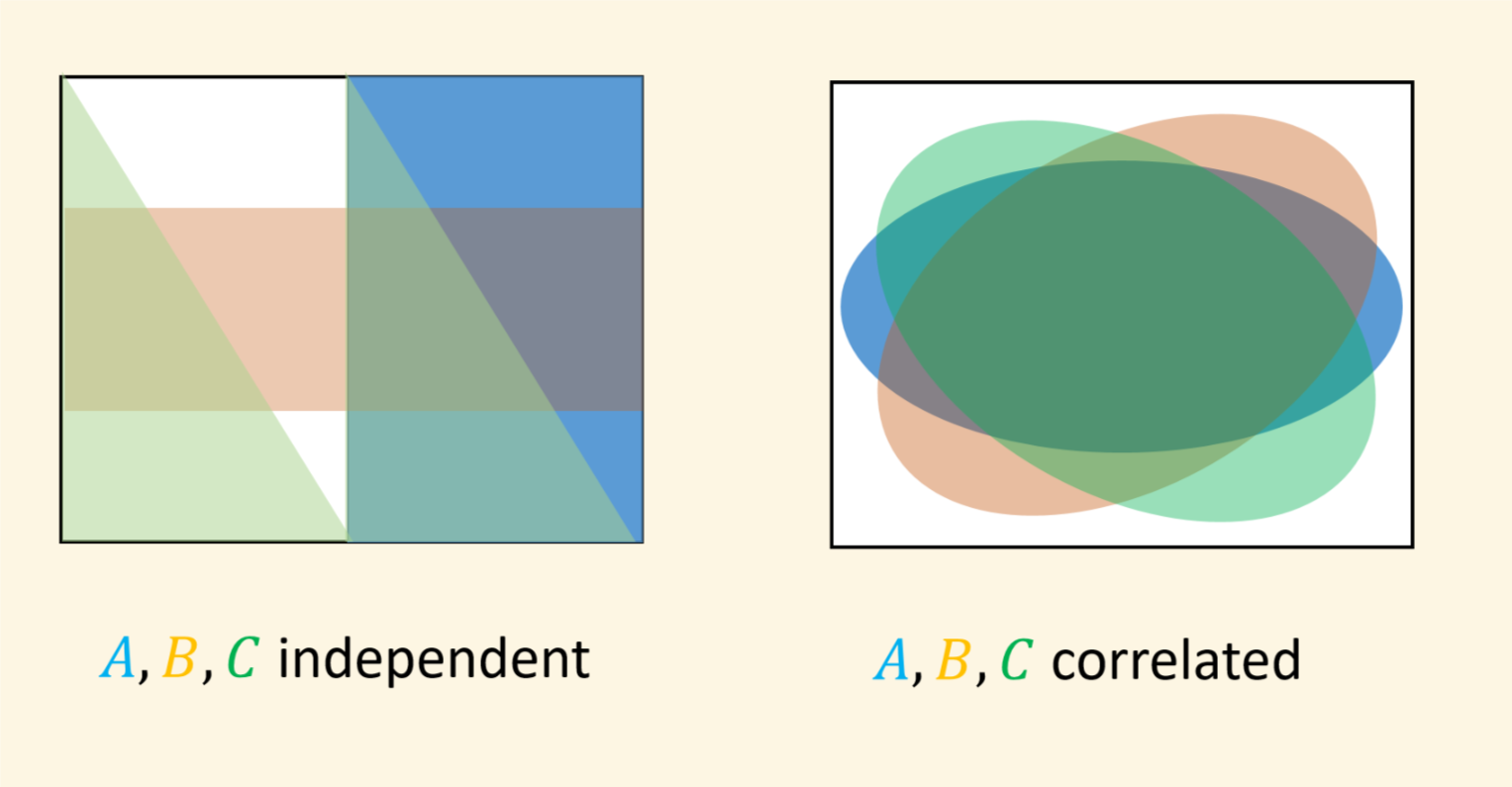
Random variables
Let \(X_0,\ldots,X_{n-1}\) be i.i.d \(0/1\) r.v.’s such that \(\mathbb{P}[X_i=1]=1/2\) for every \(i\).
Let \(Y_0,\ldots,Y_{n-1}\) be perfectly correlated \(0/1\) r.v.’s such that \(\mathbb{P}[Y_i=1]=1/2\) for every \(i\).
Which of following is true:
a. \(\mathbb{E}[X] \gt \mathbb{E}[Y]\)
b. \(\mathbb{E}[X] \lt \mathbb{E}[Y]\)
c. \(\mathbb{E}[X]=\mathbb{E}[Y]\) but \(\mathbb{P}[ |X-\mathbb{E}[X]| \gt n/4 ] \gt \mathbb{P}[ |Y - \mathbb{E}[Y] | \gt n/4 ]\)
d. \(\mathbb{E}[X]=\mathbb{E}[Y]\) but \(\mathbb{P}[ |X-\mathbb{E}[X]| \gt n/4 ] \lt \mathbb{P}[ |Y - \mathbb{E}[Y] | \gt n/4 ]\)
Random variables
Let \(X_0,\ldots,X_{n-1}\) be i.i.d \(0/1\) r.v.’s such that \(\mathbb{P}[X_i=1]=1/2\) for every \(i\).
Let \(Y_0,\ldots,Y_{n-1}\) be perfectly correlated \(0/1\) r.v.’s such that \(\mathbb{P}[Y_i=1]=1/2\) for every \(i\).
Which of following is true:
a. \(\mathbb{E}[X] \gt \mathbb{E}[Y]\)
b. \(\mathbb{E}[X] \lt \mathbb{E}[Y]\)
c. \(\mathbb{E}[X]=\mathbb{E}[Y]\) but \(\mathbb{P}[ |X-\mathbb{E}[X]| \gt n/4 ] \gt \mathbb{P}[ |Y - \mathbb{E}[Y] | \gt n/4 ]\)
d. \(\mathbb{E}[X]=\mathbb{E}[Y]\) but \(\mathbb{P}[ |X-\mathbb{E}[X]| \gt n/4 ] \lt \mathbb{P}[ |Y - \mathbb{E}[Y] | \gt n/4 ]\)
Random variables
Let \(X_0,\ldots,X_{n-1}\) be i.i.d \(0/1\) r.v.’s such that \(\mathbb{P}[X_i=1]=1/2\) for every \(i\).
Let \(Y_0,\ldots,Y_{n-1}\) be perfectly correlated \(0/1\) r.v.’s such that \(\mathbb{P}[Y_i=1]=1/2\) for every \(i\).
Which of following is true:
a. \(\mathbb{E}[X] \gt \mathbb{E}[Y]\)
b. \(\mathbb{E}[X] \lt \mathbb{E}[Y]\)
c. \(\mathbb{E}[X]=\mathbb{E}[Y]\) but \(\mathbb{P}[ |X-\mathbb{E}[X]| \gt n/4 ] \gt \mathbb{P}[ |Y - \mathbb{E}[Y] | \gt n/4 ]\)
d. \(\mathbb{E}[X]=\mathbb{E}[Y]\) but \(\mathbb{P}[ |X-\mathbb{E}[X]| \gt n/4 ] \lt \mathbb{P}[ |Y - \mathbb{E}[Y] | \gt n/4 ]\)
\(\mathbb{E}[X] = \sum \mathbb{E}[X_i] = n(1/2)= n/2\)
\(\mathbb{E}[Y] = \sum_i \mathbb{E}[Y_i] = n(1/2)=n/2\).
\(\mathbb{P}[|Y-n/2| \gt n/4] = 1\).
BY Chernoff \(\mathbb{P}[|X-n/2| \gt n/4] = 2^{-\Omega(n)}\)
Chernoff Bound
Thm: If \(X_0,\ldots,X_{n-1}\) i.i.d \(0 \leq X_i \leq 1\), then
\[\mathbb{P}\bigl[ \bigl|\sum_{i=0}^{n-1}X_i - \mathbb{E}[\sum X_i] \bigr| \geq \epsilon n \bigr] \leq 2e^{-2\epsilon^2 n}\]
Learning / hypothesis testing interpretation: From samples of \(\mu\)-coin, rule out NULL hypothesis that coin is \(\mu -\epsilon\) after \(O(1/\epsilon^2)\) samples.
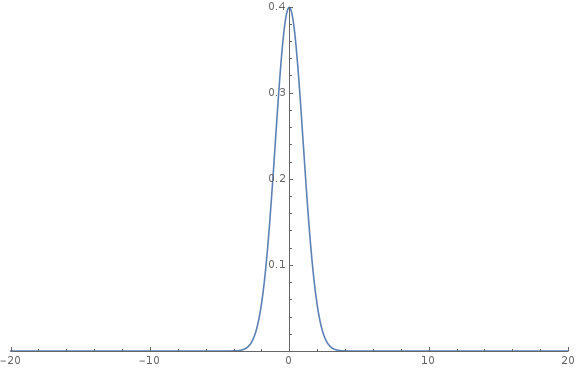
\(Var[X] = \sum Var[X_i] \leq n\). \(\sigma[X] \leq \sqrt{n}\)
\(\mathbb{P}[ |X - \mu | \gt k\sigma ] \leq exp(-k^2)\) (set \(k=\epsilon \sqrt{n}\))
Amplifying success of algorithms
Alg \(SOLVE2SAT\) finds satisfying assignment with probability at least \(0.1\).
Crucial observation: Sample space for probability is coins of the algorithm. not the inputs!
If Alg uses \(m\) coins, then for every satisfiable \(\varphi\) there is \(BAD_{\varphi} \subseteq \{0,1\}^m\) s.t.
\(|BAD| \leq 0.9 \cdot 2^m\)
\(r \not\in BAD_\varphi\) then \(SOLVE2SAT(\varphi;r)\) satisfies \(\varphi\).
Corollary: If we repeat \(k\) times with independent coins then will find sat assignment with prob at least \(1-0.9^k\).
Proof: Choose independent \(r_0,\ldots,r_{k-1} \in \{0,1\}^m\), and let \(B_i\) event that \(r_i \in BAD_\varphi\).
\(B_0,\ldots,B_{k-1}\) depend on disjoint coins \(\Rightarrow\) are mutually independent
\(\mathbb{P}[B_0 \wedge B_1 \wedge \cdots \wedge B_{k-1} ] \leq 0.9^k\).
Amplifying algorithms with two-sided error
Thm: Suppose \(ALG\) is probabilistic alg s.t. for every \(x\), \(\mathbb{P}[ALG(x)=F(x)] \geq 2/3\). where probability is over the coins of \(ALG\) Then if we run \(ALG(x)\) \(k\) independent times, \(\mathbb{P}[ \text{majority answer is $F(x)$}]\gt1-2e^{-0.01k}\)
Proof: Fix \(x\in \{0,1\}^*\), and define \(X_i=1\) if run \(i\) of \(ALG(x)\) is correct. \(X_i=0\) otherwise. Then \(X_0,\ldots,X_{k-1}\) i.i.d with \(\mu = \mathbb{E}[X_i]\geq 2/3\)
By Chernoff \(\mathbb{P}[ | \sum_{i=0}^{k-1} X_i - \mu | \gt \epsilon k ] \leq 2e^{-\epsilon^2 k/2}\)
Since \(\mu \geq (2/3)k\), to get majority wrong \(\epsilon \gt 1/6\). Comes out to \(2e^{-k/72}\).
Bonus: Proof of Paley-Zigmund
Thm: For \(Y\geq 0\), let \(\mu = \mathbb{E}[Y]\) and \(p=\mathbb{P}[ Y \geq \epsilon \mathbb{E}Y ]\) then \(p \geq (1-\epsilon)^2\tfrac{\mu^2}{\mathbb{E}[Y^2]}\).
Proof: Let \(\mu = \mathbb{E}Y\) and \(Z = \begin{cases} 1 & Y \geq \epsilon\mu \\ 0 & \text{otherwise} \end{cases}\). \(p=\mathbb{E}[Z]\)
\(\mu = \mathbb{E}[Y] = \mathbb{E}[Y(Z+(1-Z))] = \mathbb{E}[YZ] + \mathbb{E}[Y(1-Z)]\) \(\leq \mathbb{E}[YZ] + \epsilon \mu\) \(\leq \sqrt{\mathbb{E}[Y^2]^{1/2}\mathbb{E}[Z^2]}+\epsilon \mu\)
Since \(Z=Z^2\) and \(\mathbb{E}[Z]=p\) we get
\(\sqrt{\mathbb{E}[Y^2]\cdot p} \geq \mu - \epsilon\mu = (1-\epsilon)\tfrac{\mu^2}{\mathbb{E}[Y^2]}\)
Drunkard’s walk
Thm: \(\mathbb{P}[ \text{position after $n$ steps} \gt \sqrt{n}/10 ] \geq 1/10\)
Proof: Follows from Paley Zygmund inequality: for \(Y\geq 0\), \(0 \leq \epsilon \leq 1\), \(\mathbb{P}[ Y \geq \epsilon \mathbb{E}Y ] \geq (1-\epsilon)^2\tfrac{\mathbb{E}[Y]^2}{\mathbb{E}[Y^2]}\).
Use that for \(Y = (\sum X_i)^2\), \(\epsilon = 1/100\), together with \((*) \mathbb{E}[Y^2]=\mathbb{E}[X^4]=3n^2\).
Proof of \((*)\):
\(\mathbb{E}[Y^2] = \mathbb{E}[ (\sum_i X_i)^4] = \mathbb{E}[\sum_{i,j,k,\ell}X_iX_jX_kX_\ell]\) \(\sum_{i,j,k,\ell}\mathbb{E}[X_iX_jX_kX_\ell]\)
\(\mathbb{E}[X_iX_jX_kX_\ell]=1\) iff \(i=j\) and \(k=\ell\) or \(i=k\) and \(j=\ell\) or \(i=\ell\) and \(j=k\).
\(\mathbb{E}[Y^2] = 3\sum_{a=0}^{n-1}\sum_{b=0}^{n-1} 1 = 3n^2\)
Hence \(\mathbb{P}[Y \geq n/100 ] \geq 0.99^2 \tfrac{n^2}{3n^2} \sim 0.32\)