N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 20: Modeling randomized algorithms
Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow)

Laptops/phones only on last 5 rows please.
Announcements
Coding assignment: Delay deadline
Going deeper:
Salil Vadhan: Pseudorandomness (on his website)
CS 221 Madhu Sudan
CS 127 / 227 , MIT 6.857 / 6.875[J] , MIT 6.858.
Today
The class \(\mathbf{BPP}\).
What we know about its power - relations with other classes.
\(\mathbf{BPP} \subseteq \mathbf{P_{/poly}}\)
If \(\mathbf{P} = \mathbf{NP}\) then \(\mathbf{BPP}=\mathbf{P}\)
Pseudorandom generators
Question
Which one of the following conditions is not equivalent to \(F\in \mathbf{BPP}\):
a \(\exists\) poly-time RNAND<< \(P\) s.t. \(\forall_{n \in \mathbb{N}, x\in \{0,1\}^n}\), \(\mathbb{P}[P(x)=F(x)] \geq 2/3\)
b \(\exists\) poly-time RNAND<< \(P\) s.t. \(\forall_{n \in \mathbb{N}, x\in \{0,1\}^n}\) \(\mathbb{P}[P(x)=F(x)] \geq 0.51\)
c \(\exists\) poly-time RNAND<< \(P\) s.t. \(\forall_{n \in \mathbb{N}}\) , \(\mathbb{P}_{x \sim \{0,1\}^n}[P(x)=F(x)] \geq 2/3\)
d \(\exists\) poly-time NAND<< \(P'\) and poly \(p\) s.t. \(\forall_{n \in \mathbb{N}, x\in \{0,1\}^n}\) , \(\mathbb{P}_{r \sim \{0,1\}^{p(n)}}[ P(xr) = F(x) ] \geq 0.99\)
Question
Which one of the following conditions is not equivalent to \(F\in \mathbf{BPP}\):
a \(\exists\) poly-time RNAND<< \(P\) s.t. \(\forall_{n \in \mathbb{N}, x\in \{0,1\}^n}\), \(\mathbb{P}[P(x)=F(x)] \geq 2/3\)
b \(\exists\) poly-time RNAND<< \(P\) s.t. \(\forall_{n \in \mathbb{N}, x\in \{0,1\}^n}\) \(\mathbb{P}[P(x)=F(x)] \geq 0.51\)
c \(\exists\) poly-time RNAND<< \(P\) s.t. \(\forall_{n \in \mathbb{N}}\) , \(\mathbb{P}_{x \sim \{0,1\}^n}[P(x)=F(x)] \geq 2/3\)
d \(\exists\) poly-time NAND<< \(P'\) and poly \(p\) s.t. \(\forall_{n \in \mathbb{N}, x\in \{0,1\}^n}\) , \(\mathbb{P}_{r \sim \{0,1\}^{p(n)}}[ P(xr) = F(x) ] \geq 0.99\)
The class BPP
Def 1: \(F\in \mathbf{BPP}\) if there is poly-time RNAND<< prog \(P\) s.t.
\[\forall x\in \{0,1\}^*, \mathbb{P}[ P(x)=F(x)] \geq 2/3\]
Def 2: \(F\in \mathbf{BPP}\) if there is \(G\in \mathbf{P}\) and poly \(p(\cdot)\) s.t.
\[\forall x\in \{0,1\}^* \mathbb{P}_{r \sim \{0,1\}^{p(|x|)}}[ G(xr) = F(x) ] \geq 2/3\]
Thm: Both definitions equivalent
What do we know
- \(\mathbf{P} \subseteq \mathbf{BPP} \subseteq \mathbf{EXP}\)
- \(\mathbf{NP} \subseteq \mathbf{BPP}\) essentially “as good as” \(\mathbf{P}=\mathbf{NP}\).
- \(\mathbf{BPP} \subseteq \mathbf{P_{/poly}} = \cup_{a\in \mathbb{N}} SIZE(n^a)\)
- Initial conjecture: \(\mathbf{P} \subsetneq \mathbf{BPP} \subsetneq \mathbf{EXP}\)
- These days: Common belief is that \(\mathbf{P}=\mathbf{BPP}\).
Powerpoint
Hardness vs Randomness

Hardness vs Randomness
Any sufficiently advanced technology is indistinguishable from magic., Arthur C. Clarke
Any sufficiently complex function is indistinguishable from random.
“randomness” = “unpredictability” = “hard to compute”
Mathematically: theorems of form “If \(\exists\) hard \(F\) with property \(X\) then \(\exists\) pseuorandom generators with parameters \(Y\)”
Pseudorandom generator
Template Def: A psuedorandom generator is function \(G\) satisfying:
- \(G\) is “efficiently computable”
- \(|\text{output}| \gt |\text{input}|\)
- \(G(\text{random input})\) “looks random”: For every “not complicated test” \(P\),
Input known as “seed”
Question
Which of the following changes makes a pseudorandom generator weaker:
a Making the seed (i.e., input) shorter
b Making the output longer
c Making the test take more time to compute.
d Making the generator take more time to compute.
Question
Which of the following changes makes a pseudorandom generator weaker:
a Making the seed (i.e., input) shorter
b Making the output longer
c Making the test take more time to compute.
d Making the generator take more time to compute.
Formal def
Def: \(G\) is \((T,\epsilon)\)-PRG if:
\((x,i) \mapsto G(x)_i\) is poly-time computable
For every NAND prog \(P\) of \(\leq T\) lines:
Optimal PRG Conj: \(\exists\) \(\delta\gt0\) and \((2^{\delta \ell},2^{-\delta \ell})\) generator \(G:\{0,1\}^\ell \rightarrow \{0,1\}^m\) for every \(m\lt2^{\delta \ell}\).
Optimal PRG leads to BPP=P
Intuition:
- Reduce coins from \(m\) to \(\ell = O(\log m)\) using PRG.
- Enumerate over all possible coins.
Optimal PRG leads to BPP=P
Thm: If Optimal PRG conj true then \(\mathbf{BPP}=\mathbf{P}\).
Pf: Let \(F\in \mathbf{BPP}\), \(P\) time \(p(n)\) s.t. \(\forall_{x\in \{0,1\}^n}\mathbb{P}_{r\sim \{0,1\}^m}[ P(x;r)=F(x)] \geq 2/3\)
CLAIM: If \(G:\{0,1\}^\ell \rightarrow \{0,1\}^m\) is \((T,0.1)\) PRG and \(T \gg p(n)\) then \(\color{green}{\mathbb{P}_{s \sim \{0,1\}^\ell}[ P(x;G(s))=F(x)]} \geq 0.51\) for ever \(x\in \{0,1\}^n\).
PF of CLAIM: Suppose otherwise, let \(x^*\) violating example. \(r \mapsto P(x^*;r)\) is in \(SIZE(O(p(n)))\) \(|2/3-0.51| \gt0.1\) \(\color{red}{\Rightarrow}\) contradiction!
Pf of Thm: Compute \(\color{green}{p=\mathbb{E}_{s \sim \{0,1\}^\ell}[ P(x;G(s))]}\) in \(O(2^\ell p(n))\) time. Output \(1\) iff \(p\gt1/2\).
The power of randomness
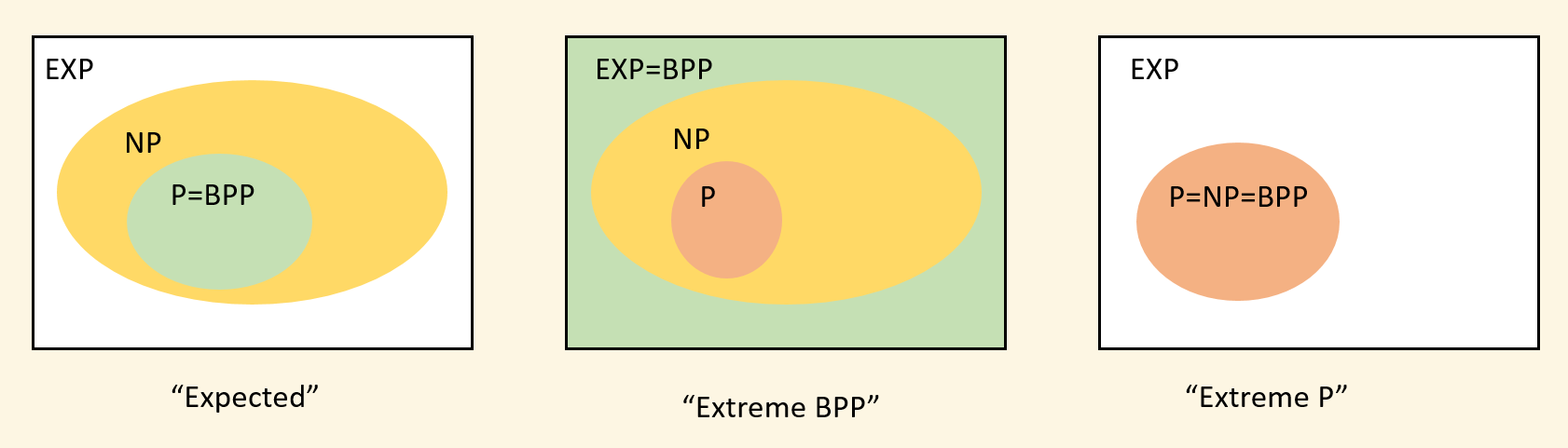
\(\mathbf{BPP}\) and \(\mathbf{NP}\)
Thm: If \(\mathbf{NP} \subseteq \mathbf{BPP}\) then there are no non-trivial pseudorandom generators.
Sketch: In this case can test given \(r\) if \(\exists_s\) s.t. \(R=G(s)\).
BPP and NP
Thm: If \(P=NP\) then \(BPP=P\).
Proof idea: Let \(P\) be probabilistic algorithm using \(m\) coins and success \(1-2^{-k}\).
Define \(Q(x) = \exists_{s_0,\ldots,s_{10m/k}} \forall_{r\in \{0,1\}^m} P(x;s_i \oplus r)=1\).
Let \(R_x \subseteq \{0,1\}^m\) be s.t. \(P(x;r)=1\) for all \(r\in R_x\).
If \(|R_x|\lt k/(10m)\) then \(Q(x)=0\).
If \(|R_x| \gt (1-2^{-k})2^m\) then for every \(y\in \{0,1\}^m\), \(\mathbb{P}[ y\not\in s \oplus R_x ] \lt 2^{-k}\).