\renewcommand{}{}
N or Space for next slide, P for previous slide, F for full screen, M for menu
Lec 21: Crypto
Boaz Barak (instructor), Salil Vadhan (co-instructor), Juan Perdomo (Head TF).
Team: Aditya Mahadevan, Brian Sapozhnikov (surveys), Chan Kang (extension), Gabe Abrams (Ed Tech), Gabe Montague (NAND web), Jessica Zhu (proof workshops), John Shen, Juan Esteller (NAND implementation), Karl Otness, Katherine Binney, Mark Goldstein (clicker expert), Stefan Spataru, Susan Xu, Tara Sowrirajan (mushroom forager), Thomas Orton (Advanced Section)
Slides will be posted online.

Laptops/phones only on last 3 rows please.
Announcements
CS 127 / 227 , MIT 6.857 / 6.875[J] , MIT 6.858.
Reading posted tomorrow or sat.
HW10 due date: Tuesday after Thanksgiving
“HW11” due sometime in reading period
Crypto 3000BC - 1970AD
- Alice designs encryption scheme, proclaims it “unbreakable”
- Bob uses Alice’s encryption to send a message to Charlie.
- Dorothy breaks the “unbreakable” crypto scheme.
- Bob loses head.
- Alice designs new version of encryption. Proclaims it “unbreakable”
Modern crypto
Use Definitions and Reductions
Prototypical Def: Scheme \(S\) satisfies security notion \(X\) if for every ptime adversary \(A\), \(\mathbb{P}[ \text{$A$ succeeds in $X$ attack on $S$}] \lt \tfrac{1}{poly}\).
Prototypical Thm: If problem \(P\) is hard
then scheme \(S\) is \(X\)-secure.
End result: Encryptions scheme that withstood unrecedent attacks. Security goals that people never dared to imagine.
Reality check
If crypto is so great, how come things get hacked all the time?

Reality check
If crypto is so great, how come things get hacked all the time?

Today
Perfect secrecy
Necessity of long keys
Computational secrecy and derandomized one-time pad (stream cipher)
Breaking crypto if P=NP
Public key cryptography
Definition of encryption
Def \((E,D)\) valid if efficient \(D_k(E_k(x))=x\) for every \(k\in \{0,1\}^*\), \(x\in \{0,1\}^*\) \(D_k(E_k(x))=x\)
Parameters: \(n\)=key length, \(L\)=plaintext length
Question: For which of the following \(E:\{0,1\}^n \times \{0,1\}^n \rightarrow \{0,1\}^*\) there is no \(D\) that makes it valid?
a. \(E_k(x) = (x_0 \oplus k_0, x_1 \oplus k_1, \ldots, x_{n-1} \oplus k_{n-1})\)
b. \(E_k(x)=x\)
c. \(E_k(x)= (x+y) \mod 2^n\) (thinking of \(x,y\) as numbers)
d. \(E_k(x) = (x_0 \wedge k_0, x_1 \wedge k_1, \ldots, x_{n-1} \wedge k_{n-1})\)
Encryption (graph view)
For every \(k\in \{0,1\}^n\), \(\{ (x,E_k(x)) \}\) is matching of \(2^L\) edges.
“Simple” encryption: no parallel edges (\(E_k(x)\neq E_{k'}(x)\) for \(k\neq k'\))
Security
“Perfect Secrecy” is defined by requiring of a system that after a cryptogram is intercepted by the enemy the a posteriori probabilities of this cryptogram representing various messages be identically the same as the a priori probabilities of the same messages before the interception., Claude Shannon, 1949
Game:
- Messages \(x_0,x_1,\ldots,x_{m-1}\) with probabilities \(p_0,\ldots,p_{m-1}\)
- Choose \(i \in [m]\) with probability \(p_i\) and output \(y=E_{k\sim \{0,1\}^n}(x_i)\)
- If system is perfectly secret then for every \(y^* \in \{0,1\}^*\) and \(i^*\in [m]\), \(\mathbb{P}[ i=i^* | y=y^* ] = p_{i^*}\).
Intuition: If \(E_{k \sim \{0,1\}^n}(x_7) \equiv E_{k \sim \{0,1\}^n}(x_{12})\) then observing \(y\) doesn’t help to tell if \(i=7\) or \(i=12\).
Perfect Secrecy
Def: \((E,D)\) is perfectly secret if for every \(x,x' \in \{0,1\}^L\), \(E_{k \sim \{0,1\}^n}(x) \equiv E_{k \sim \{0,1\}^n}(x')\).
i.e., for every \(y\in \{0,1\}^*\),\(\color{green}{\mathbb{P}_{k\sim \{0,1\}^n}[y=E_k(x)]= \mathbb{P}_{k\sim \{0,1\}^n}[y=E_k(x')]}\)
Graph view: Simple \((E,D)\) is perfectly secret iff \(Neighbors(x)=Neighbors(x')\) for every \(x,x'\).

Intuition: Every ciphertext equally likely to come from all plaintexts.
One time pad
Thm There is perfectly secret encryption with \(L=K\).
Proof: Identify \(\{0,1\}^n\) with \(\mathbb{Z}_{2^n}\) or \(\mathbb{Z}_2^n\).
\(E_k(x)= (x+k)\), \(D_k(y)=y-k\).
\(D_k(E_k(x))= (x+k)-k=x\).
CLAIM: Graph is complete bipartite graph. For every \(x,y \in \{0,1\}^n\), there is exactly one edge \(k=x-y\).
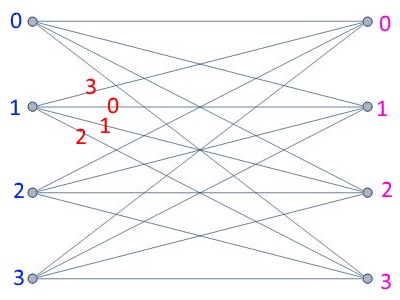
Necessity of long keys
Thm: If \((E,D)\) is perfectly secret then \(L \leq n\).
Lemma: If bipartite \(G=(V\cup U,E)\) has degree \(\lt|V|\) and contains \(|V|\) sized matching, then exist \(x, x' \in V\) with different neighbors.
Lemma \(\Rightarrow\) Theorem: Fix \(k\), then \((x,E_k(x))\) is matching.
Proof of Lemma:
Summary
Can define perfect secrecy
Perfect secrecy does guarantee security against eavesdropping adversary.
Can construct perfectly secret schemes
Schemes have terrible key length requirements
Computational Secrecy
Intuition: After seeing ciphertext \(y\), an efficient adversary gets negligible advantage over prior information.
Formal def: \((E,D)\) computational secret if \(\forall p:\mathbb{N}\rightarrow \mathbb{N}\), \(\forall\) large \(n\), if \(|P| \leq p(n)\) and \(x,x' \in \{0,1\}^{L(n)}\) then
Computational Indistinguishability
Perfect secrecy: \(E_{k\sim \{0,1\}^n}(x)\) and \(E_{k \sim \{0,1\}^n}(x')\) are identical
Computational secrecy: \(E_{k\sim \{0,1\}^n}(x)\) and \(E_{k \sim \{0,1\}^n}(x')\) are indistinguishable
“There are not in nature two real, absolute beings, indiscernible from each other”, Gottfried Wilhelm Leibniz “identity of indiscernibles”
Define \(Y\) and \(Y'\) are “practically identical” if can’t be distinguished by efficient algorithms.
Pseudorandom generators: \(G(\text{short random})\) is “practically identical” to \(\text{long random}\)
Encryption: \(E_{\text{random}}(x)\) is “practically identical” to \(E_{\text{random}}(x')\)
Notation: \(U_n\): uniform over \(\{0,1\}^n\), above is \(E_{U_n}(x) \approx E_{U_n}(x')\)
Computational Indistinguishability
Def: Two distributions \(Y, Y'\) over \(\{0,1\}^m\) are \((T,\epsilon)\)-close if \(\forall\) NAND prog \(Q\) of at most \(T\) lines
Problem: Write def of \((T,\epsilon)\) PRG \(G:\{0,1\}^n \rightarrow \{0,1\}^L\) in these terms.
Solution: \(G\) is \((T,\epsilon)\) PRG if \(G(U_n)\) and \(U_L\) are \((T,\epsilon)\) close.
Def: \((E,D)\) is comp secret if \(\forall\) poly \(p\) , large enough \(n\), \(x,x' \in \{0,1\}^{L(n)}\), \(E_{U_n}(x)\) is \((p(n),\tfrac{1}{p(n)})\) close to \(E_{U_n}(x')\)
C.I. Paradigm
If \(Y \approx Z\) then \(Z\) “just as good” as \(Y\).

Derandomized one-time pad:
- Start with scheme secure with long random key
- Replace with pseudorandom string derived from short key
- Argue replacement is just as good.
Derandomized One Time Pad
Ingredient: \(G:\{0,1\}^n \rightarrow \{0,1\}^L\)
Encryption: \(E_k(x) = x+G(k)\), \(D_k(y) = y - G(k)\).
Thm: For every poly \(p(n)\), and \(x,x' \in \{0,1\}^{L(n)}\), \(E_{U_n}(x)\) \((p(n),\tfrac{1}{p(n)})\)-close to \(E_{U_n}(x')\).
Proof:
Public Key Encryption
“Obvious”: Alice and Bob need to exchange secret key before communicating
“Proof”: To send message \(x\) to Alice, Bob needs to know key \(k\) to compute \(y=E_k(x)\). But if \(k\) is sent “in clear” then Eve can compute \(x=D_k(y)\)
Subtle assumption: Same key used for encrypting and decrypting!
Diffie-Hellman / Merkle / Ellis 1970’s: Doesn’t need to be the case!
Today: Absolutely essential for online security.
Diffie-Hellman Key Exchange
- Alice: Chooses \(g,a\), sends \(g,g^a\)
- Bob: Given \(g,h\) chooses \(b\), sends \(g^b,h^b + x\).
- Alice: Given \(e,y\) outputs \(y^a - y\).
- DDH Assumption \((g,g^a,g^b,g^{ab}) \approx (g,g^a,g^b,\text{random})\)