\renewcommand{}{}

N or Space for next slide, P for previous slide, F for full screen, M for menu

You might need to press C (possibly twice) to be able to click on links.

Lec 25: Quantum

Boaz Barak (instructor), Brian Sapozhnikov (Head TF), Albert Chalom, Alexis Ross, Charles O’Mara, Daniel Chen, David Li , Jambay Kinley, Jane Ahn, John Shen, Josh Seides, Laura Pierson, Pranay Tankala, Raymond Lin, Theresa Nguyen, Wanqian Yang, William Fu, Hikari Sorensen (Extension TF), Eric Lu (Patel Fellow)

Laptops/phones only on last 5 rows please.

Quantum Mechanics

Interference positive and negative probabilities.
Measurement (non commutativity): measuring a property collapses it.
Entanglement measuring one system can affect another.
Uncertainty / no cloning Can’t get all information about a system.

Buzzwords:

Move from probabilities to amplitudes

Usually same thing when talking about large systems \((\pm \alpha_0 \pm \alpha_1 \cdots \pm \alpha_m)^2 \approx \alpha_0^2 + \alpha_1^2 + \cdots + \alpha_m^2\)

99% of CS theory and practice stays the same but 1% part is quite interesting

Question

If we shoot baseballs through two slits, what’s the pattern that we expect to see?

Double slit experiment

Quantum weirdness II: Bell’s Inequalty

We give a random \(x \in \{0,1\}\) to Alice and get response \(a \in \{0,1\}\), and random \(y\in \{0,1\}\) to Bob and get response \(b\). If \(x=y=1\) then they win if \(a\neq b\). Otherwise they win if \(a=b\)

Thm 1: Every classical strategy wins with probability \(\leq 0.75\).

Thm 2 (+experiments): If Alice and Bob can share entangled qubits then they can win with probability \(\tfrac{1}{2} + \tfrac{1}{2\sqrt{2}} \geq 0.85\).

Bell’s Inequality

Measurement Problem

Is there a problem?

What’s the goal of a physical theory?

Predict results of experiments?

Give a “story” on what’s really out there?

What sorts of stories are allowed?

Panel moderated by Brian Greene

Quantum Computing: Abbreviated history

1981: Feynman talks on difficulty of simulating quantum systems. Speculates on a “different type of computer”

1985: David Deutsch turns observation on its head. Suggest this as attack on Extended Church Turing Thesis.

1993: Bernstein and Vazirani give more rigorous definitions. First formal evidence of exponential speedup (building on Deutsch-Josza).

1994: Simon gives “period finding” algorithm over \(\mathbb{Z}_2^n\).

1994 (later): Shor gives “period finding” algorithm for \(\mathbb{Z}_{N}\), uses this to obtain factoring and discrete logarithms.

Field explodes

Current status

Strong experimental progress toward building \(50-100\) qubit machines. Known as Noisy Intermediate Scale Quantum (NISQ) computers. (Compare with \(\approx 10^{12}\) bits on high-end iPhone)

Current goal: “quantum superiority”. Solve problem on fridge-size quantum computer that requires\(^*\) datacenter-size classical computer.

Scalable quantum computers realistic enough to transition away from RSA / Diffie Hellman / ECC.

Quantum computers seem unlikely to help with \(\mathbf{NP}\) complete problems.

Non crypto applications: quantum chemistry, machine learning(?)

Complexity classes

\(\mathbf{BQP}\): polynomial time quantum computable functions.
\(\mathbf{BPP} \subseteq \mathbf{BQP} \subseteq \mathbf{EXP}\).

Believed that \(\mathbf{BPP} \subsetneq \mathbf{BQP}\): quantum can sometimes give superpolynomial advantage.

But \(\mathbf{NP} \not\subseteq \mathbf{BQP}\): its not a silver bullet.

Executive summary

Quantum computing doesn’t change basic lessons:

Algorithms can be modeled by strings
There is a universal algorithm.
Uncomputability exactly the same
Intractability largely the same
Exciting recent progress: Use computational view to address fundamental physics questions.

Modeling quantum algorithms

Quantum system

State of \(n\) qubit system: unit vector \(v\) of dimension \(2^n\). Coordinates identified with \(\{0,1\}^n\).
Evolution: Apply unitary matrix \(U\): \(v \leftarrow Uv\).
Gates: Unitary matrices that only modify \(\leq 3\) qubits.
Measurement: Observe \(x \in \{0,1\}^n\) with probability \(|v_x|^2\).

Quantum computing on three bits

System state: \(v \in \mathbb{R}^8\), \(\|v\|=1\). \(v = v_{000}\color{red}{|000\rangle} + v_{001}\color{red}{|001\rangle} + v_{010}\color{red}{|010\rangle} + \cdots + v_{111}\color{red}{|111\rangle}\)

\(\color{red}{|010\rangle} = \left( \begin{smallmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{smallmatrix} \right)\)

Operation: \(v \mapsto Uv\), \(U\) is \(8\times 8\) unitary matrix.

Example: Apply \(H = \tfrac{1}{\sqrt{2}} \left( \begin{smallmatrix} +1&+1\\ +1&-1 \end{smallmatrix} \right)\) to first bit

\(Hv = v_{000}(H\color{red}{|0\rangle})\color{red}{|00\rangle} + v_{010}(H\color{red}{|0\rangle})\color{red}{|10\rangle} + \cdots + v_{110}(H\color{red}{|1\rangle})\color{red}{|10\rangle} + v_{111}(H\color{red}{|1\rangle})\color{red}{|11\rangle}\)

\(=\tfrac{1}{\sqrt{2}}\Bigl( v_{000}(\color{red}{|000\rangle} \color{green}{+} \color{red}{|100\rangle}) + v_{010}(\color{red}{|010\rangle} \color{green}{+} \color{red}{|110\rangle}) + \cdots\) \(+ v_{110}(\color{red}{|010\rangle} \color{green}{-} \color{red}{|110\rangle}) + v_{111}(\color{red}{|011\rangle} \color{green}{-} \color{red}{|111\rangle}) \Bigr)\)

Measurement: Get value \(abc \in \{0,1\}^3\) with probability \(v_{abc}^2\).

Example: \(v = \color{red}{|111\rangle}\), and apply \(H\) to each bit

\(\tfrac{1}{\sqrt{8}}\) \((\color{red}{|0\rangle} - \color{red}{|1\rangle})(\color{red}{|0\rangle} - \color{red}{|1\rangle})(\color{red}{|0\rangle} - \color{red}{|1\rangle})\)

\(=\tfrac{1}{\sqrt{8}}\bigl(\color{red}{|000\rangle} - \color{red}{|001\rangle} - \color{red}{|010\rangle} + \color{red}{|011\rangle} - \color{red}{|100\rangle} + \color{red}{|101\rangle} + \color{red}{|110\rangle} - \color{red}{|111\rangle} \bigr)\)

If measure, get each outcome \(abc \in \{0,1\}^3\) with probability \((\pm \tfrac{1}{\sqrt{8}})^2 = \tfrac{1}{8}\).

QNAND

Operations are

foo = NAND(bar,blah) (corresponds to \(foo \leftarrow foo \oplus NAND(bar,blah)\))
Had(foo) (correspond to \(foo \leftarrow Had(foo)\))

Run \(s\) line prog on input \(x\):

Initialize to state \(x0^{n-1}\) (i.e. \(v = \color{red}{|x0^{n-1}\rangle}\) vector in \(\mathbf{R}^{2^s}\) )

Run line by line, get \(v^* = U_{s-1}U_{s-2}\cdots U_1U_0v\).

measure, get \(z\in \{0,1\}^s\) w.p. \(|v^*_z|^2\).

Output \(z^{s-m},z^{s-m+1},\ldots,z^{s-1}\) (where \(m\) = num of outputs)

Quantum algorithm - recipe

Get input \(x \in \{0,1\}^n\)

Create quantum state \(v\in \{0,1\}^{2^{poly(n)}}\) where “undesirable values” cancel out.

Measure \(v\)

Flashback to Lecture 1

Fourier Transform

In 1822 Joseph Fourier proposed solution to “heat equation” using following observation:
Every (“nice”) \(f:[0,1] \rightarrow \mathbb{R}\) can be decomposed as a sum of wave functions of the form \(g(x) = \sin(a x)\) or \(g(x)=\cos(b x)\).

Another example

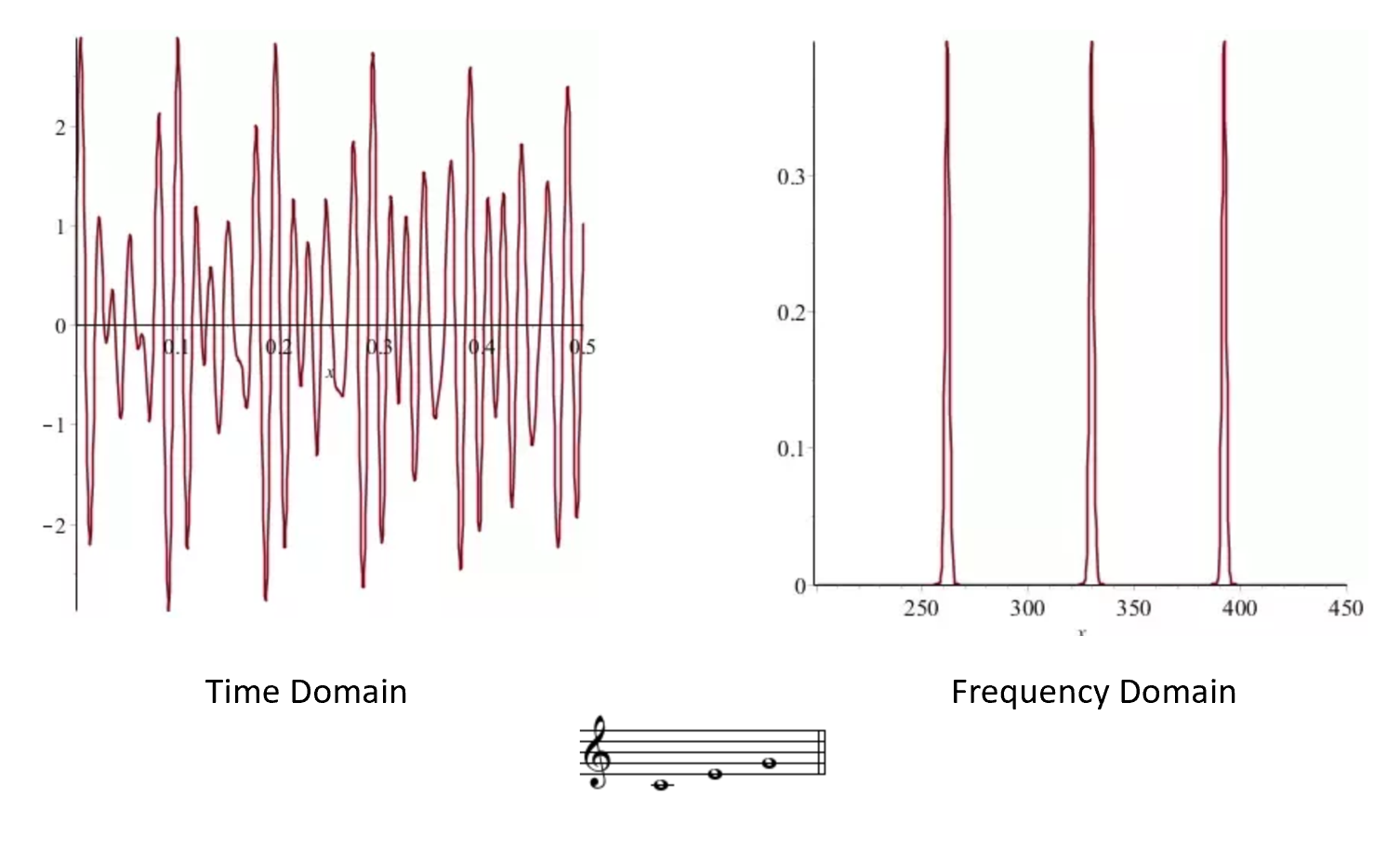
Fast Fourier transform

In 1965, Americans wanted to find way to detect Soviet nuclear experiments from seismic data. Can do so with Fourier transform but was too slow.

John Tukey came up with “Fast Fourier Transform”: improve running time from \(n^2\) to \(n \log n\): thousand or million times speedup!

Tukey couldn’t publish so collaborated with James Cooley for chemistry application.

On every “top 10 algorithms” list. Applications include signal processing, compression, spectroscopy, engineering, earth sciences, optics, crystallography,…

Fourier transform

Input: \(f:G \rightarrow \mathbb{R}\)

Output: Representation \(\hat{f} = \sum_y \hat{f}(y) \chi_y\). \(\chi_y\) is “periodic” function.

Dr. Chris Geoscience | Clare Zhang | Vi Hart | Umesh Vazirani on Quantum FT | Kelsey Houston-Edwards on Shor’s Algorithm

Shor’s Algorithm in a Nutshell

Input: \(n\)-bit integer \(m=p\cdot q\).

Find some efficient function \(f:\{0,1,\ldots, m-1\} \rightarrow \{0,1\}^*\) that is \(\varphi(m)\) periodic mod \(m\). \(\varphi(m)=(p-1)(q-1)\)

Use Quantum Fourier Transform to obtain quantum state corresponding to “\(\hat{f}\)”

Repeat several times and measure to learn period \(z=(p-1)(q-1)\).

Use equations \(pq = m\) and \((p-1)(q-1)=z\) to compute \(p,q\)

Quantum Fourier Transform over \(\mathbb{Z}_2^n\)

Given: \(f:\{0,1\}^n \rightarrow \{0,1\}\). efficiently computable function

Create: State \(\hat{f} \in \mathbf{R}^{2^n}\), \(\hat{f} = \sum_{y\in \{0,1\}^n} \hat{f}(y)\color{red}{|y\rangle}\)

\(\hat{f}(y) = \tfrac{1}{2^n}\sum_{x \in \{0,1\}^n} -1^{f(x)}(-1)^{\sum x_i y_i}\)

Quantum Fourier Transform

Initialize state to \(\color{red}{|0^n \rangle}\).
Apply \(HAD(x_i)\) to all \(i\)

\(\tfrac{1}{2^{n/2}}(\color{red}{|0\rangle} + \color{red}{|1\rangle}) (\color{red}{|0\rangle} + \color{red}{|1\rangle}) \cdots (\color{red}{|0\rangle} + \color{red}{|1\rangle})\) \(=\tfrac{1}{2^{n/2}}\sum_{x\in \{0,1\}^n}\color{red}{|x\rangle}\)

Apply \(\color{red}{|x\rangle} \mapsto -1^{f(x)}\color{red}{|x \rangle}\)

\(\tfrac{1}{2^{n/2}}\sum_{x\in \{0,1\}^n} -1^{f(x)}\color{red}{|x \rangle}\)

Apply \(HAD(x_i)\) to all \(i\)

\(\tfrac{1}{2^n}\sum_{x\in \{0,1\}^n}-1^{f(x)}(\color{red}{|0\rangle} + (-1)^{x_0}\color{red}{|1 \rangle}) \cdots (\color{red}{|0\rangle} + (-1)^{x_{n-1}}\color{red}{|1 \rangle})\)

\(=\tfrac{1}{2^n}\sum_{x\in \{0,1\}^n} \sum_{y\in \{0,1\}^n} -1^{f(x)} (-1)^{\sum y_i x_i} \color{red}{|y \rangle}\)

\(= \sum_{y\in \{0,1\}^n} \hat{f}(y)\color{red}{|y \rangle}\)

Bottom line

Can be used to discover if \(f:\{0,1\}^n \rightarrow \{0,1\}^*\) is \(\mathbb{Z}_2^n\) periodic in the sense that \(f(x \oplus z)=f(x)\)

Using ideas behind Fast Fourier Transform can do the same for group \(\mathbb{Z}_m\): find \(z\) s.t. \(f((x + z) \mod m)=f(x)\)

Other algorithms: Quantum Random Walks, Quantum Adiabatic Algorithm, Quantum Machine Learning. (Important term: \(e^{i t A}\) for matrix \(A\))

Quantum computing and crypto

Quantum computers don’t seem to effect private key cryptography.
Break factoring and discrete-log based public key systems.
Alternative: lattice based cryptography